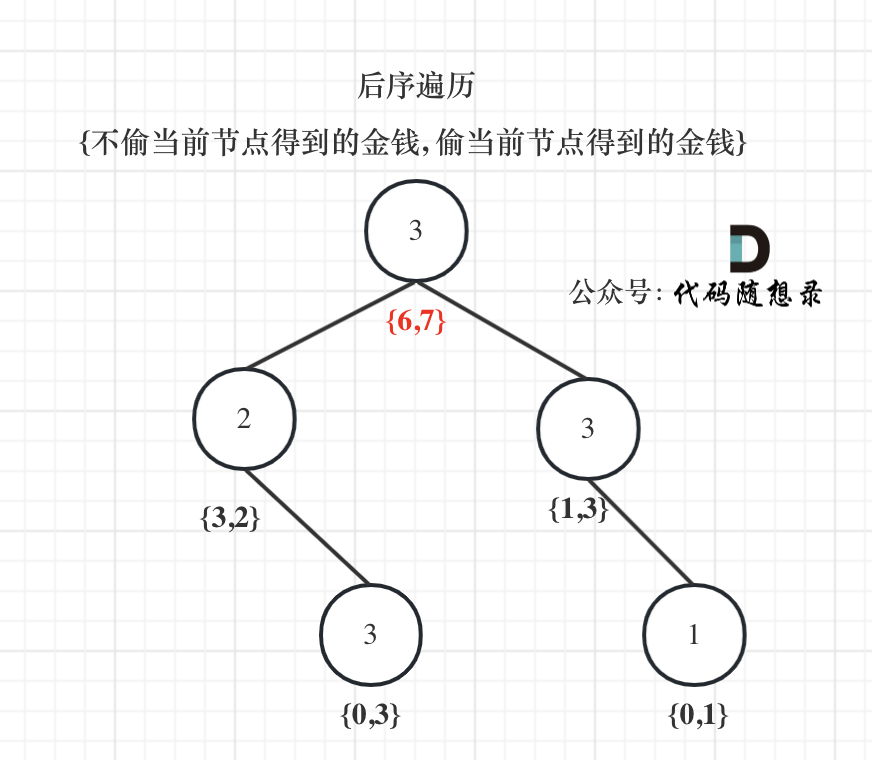
在上一节中，我们对生日问题进行了严谨的阐述：假设屋子里面每个人的生日相互独立，而且等可能的出现在一年 365 天中的任何一天，试问我们需要多少人才能让某两个人的生日在同一天的概率超过 50%。

处理抽象逻辑问题的一个入手点就是先形象化，简单化和实例化。首先不难理解一年只有 365 天，如果屋子里有366 人，那么一定有两个人的出身日期在同一天，此时概率是 100%。如果屋子里只有 1 个人，那么有两个人同一天生日的概率就是 0。试想如果屋子里有 183 人（365 的一半），这些人的生日不重复，于是这种情况将 365 天分成了相当的两部分，一部分属于那 183 人的生日，另一部分不属于 183 人的生日，此时进入第 184 人，这个人的生日只有两种可能，落入第一部分或者第二部分，由于两部分的天数一样多，那么他落入哪一部分的可能性都相同也就是 50%，如果落入第一部分，那么我们就得到两个人有相同生日的情况。由此可见，确切的答案一定在[2,184]之间。

此外解决逻辑问题，特别是算法问题，还有一种有效方法就是暴力破解。也就是我们把所有可能的情况一一罗列出来，找出合适的那个，然后再看看有没有好的方法改进暴力破解法。假设屋子里有 n 人，那么我们罗列出他们所有可能的生日情况，把这些情况中有出现重复的部分抽取出来。在简单情况下，屋子里只有 2 人，每个人的生日可能是 365 天中某一天，于是这两个人可能的生日组合是 365 * 365 = 133,225种情况（注意问题假设，屋子里人的生日相互独立）。 在这么多种组合中，两个人生日在同一天的情况有多少种呢？如果第一个人选定某一天后，第二个人必须跟他一样，由于第一个人只有 365种选择，因此两人生日相同的情况有 365 * 1 = 356 ，于是屋子里有 2 个人时，出现同一天生日的概率是 365 / (365 * 365) = 1 / 365 = 0.27%.

如果屋子里有 3 个人，那么生日情况就有 365 * 365 * 365 = 48,627, 125 种。这种情况比较复杂的是，如何考虑有两个人出现重复生日的情况，稍微大意就会出错。这里我们虽然考虑有两个人生日相同，但如果 3 个人同时生日相同，这种情况也能满足题目要求，所以不能遗漏，3 个人生日相同的情况数量就是 365 * 1 * 1 = 365种。除去 3 人同时生日相同的情况后，我们就能考虑只有 2 人生日相同的情况，如果假设前两个人生日相同，第 3 个人与前两个人不同，那么满足条件的情况就是 365 * 1 * 364 = 132,860，同理第 2 第 3 人生日相同，但第一人与后两人不同的情况也是365 * 1 * 364 = 132,860，最后第 1,3 两人生日相同，第 2 个人跟其他两个不同的情况也是365 * 1 * 364 = 132,860，由此屋子里有 3 个人，其中出现两个人生日相同的情况总数就是 132,860 + 132,860+132,860 + 365，由此对应概率就是（132,860 + 132,860+132,860 + 365）/ 48,627, 125 = 0.82%。

我们上面的枚举方法非常容易出错。要不就是多算了某种情况，要不就是少算了某种情况。例如三个人有相同生日时，我们只能将其算一次，我们不能把他看成第一第二个人生日相同算一次，然后第二第三个人生日相同算一次，然后第一第三个人生日相同又算一次，这么想我们就会将它算成 3 次。另外枚举法随着人数的增多也越来越难以使用，例如 4 个人的时候，我们要考虑只有两个人生日相同，只有三个人生日相同，4 个人生日相同等情况，还有更麻烦的情况是其中两个人生日共同在某一天，然后另外两个人生日又共同在不同的某一天，例如其中两人生日在 3 月 4 日，然后另外两人生日在 5 月 6 日等。

由此看来暴力枚举方法不是解决该问题的有效手段。在概率论上一个有效方法是从反面思考。例如我们直接考虑事件 A 的概率 p发现很难下手，那不妨先考虑非 A 的对应概率1-p,因为只要直到后者，那么前者自然迎刃而解。由此我们看看如果屋子里有 n 个人，那么他们没有人有相同生日的概率怎么算。如果每个人依次走入房间，那么第一个人进入房间时只有他自己，那么此时不可能有人跟他有相同生日，因此这时没有两人有相同生日的概率是 1, 也就是 365 / 365.第二个人接着进入，那么他的生日必须要跟第一个人不同，此时他有 364 种选择，因此此时两人生日不同的概率是 (365 / 365) * (364 / 365)，这里用到的一个原则是，两个相互独立的事件，他们同时发生的概率等于两个事件概率的乘机。根据同样的规律，第 3 个人进入房间后，他有 365-2=363 种可能使得他的生日与前两人都不同，因此 3 人没有相同生日的概率是(365 / 365) * (364 / 365) * (363 / 365)。由此可以推测 n 个人进入屋子后，没有人生日相同的概率是(365 / 365) * (364 / 365) * (363 / 365) * … ((365 - (n-1)) / 365)。

这里需要注意的是分子变化，因为分母都是 365。对应第一个人分子是 365，第二个人是 364，因此到第 n 个人时，分子变成 365-(n-1)。我们把上面的连续乘积用符号表示如下：

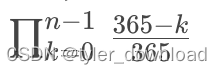
如果我们使用阶乘简化上面公式，阶乘就是 n!= n * (n-1) * … 1，需要注意的是 0! = 1。我们把上面公式展开就是：

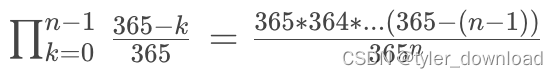
我们在分子和分母同时乘以(365-n)!，那么就有：

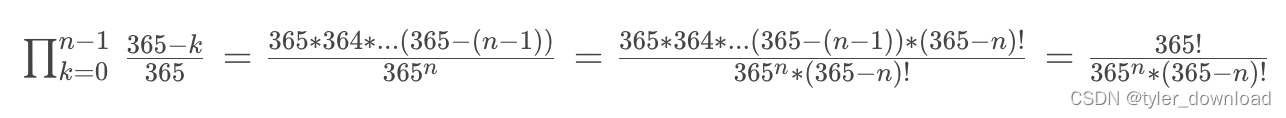
如果我们能找到一个最小的 n 值，使得上面公式计算结果小于 1/2，那么问题就能解决，因为当 n人中没有两个人的生日相同的概率小于 1/2,那么其相反事件的概率也就是至少有两人生日相同的概率就大于 1/2，如果使用 f(n)表示上面公式最右边的计算，我们用代码将它的图形画出来看看规律：

import matplotlib.pyplot as plt
import numpy as np
import mathdef no_share_birthday(n):return math.factorial(365) / (365 **n * math.factorial(365-n))x = []
for v in range(50):x.append(v)y = []
for v in x:y.append(no_share_birthday(v))plt.scatter(x, y)
plt.show()print(f"no share birthday with 22 people is :{no_share_birthday(22)}, and with 23 people is {no_share_birthday(23)}")

上面代码运行结果如下：

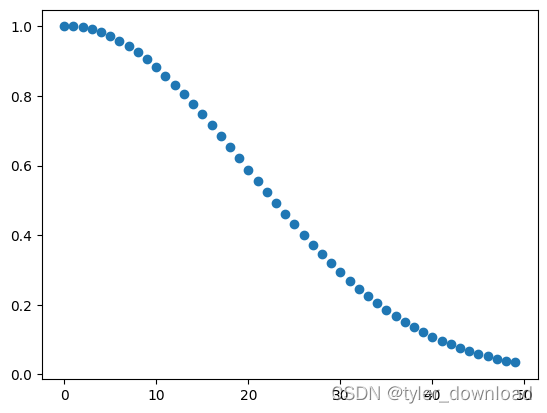
no share birthday with 22 people is :0.5243046923374499, and with 23 people is 0.4927027656760146

从绘制的图形看到随着 n 的值越大，对应两个人没有相同生日的概率逐渐减小，在 20 过去一点对应概率就在 0.5 以下，同时我们也在代码中打印出 22 人和 23 人情况下没有人有相同生日的概率，可以看到 22 人的时候概率还在 0.5 以上，到了 23 人概率正好低于 0.5，也就是说当有 23 人时，有两人生日在同一天的概率会超过0.5.

由此可见我们推导的公式可以计算对应概率，但也有问题。一是不够通用，如果一年的天数改变了，我们需要重新计算，例如在火星一年有 687 天，那么房间需要多少火星人才能让其中两个人生日同一天的概率大于 0.5 呢。另外上面的计算公式不够简洁，我们是否能推导出一个好看的数学公式来直接算出相应概率呢，我们下一节看看如何实现这些目标。更多内容请在 b站搜索 coding 迪斯尼。