581. 最短无序连续子数组

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的 最短 子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

示例 2：

输入：nums = [1,2,3,4]
输出：0

示例 3：

输入：nums = [1]
输出：0

提示：

$1<=nums.length<=10^4$
$-10^5<=nums[i]<=10^5$

进阶：你可以设计一个时间复杂度为 O(n) 的解决方案吗？

最简单的方法就是排序后，比较相同元素的数量，但我竟然没想到 = =。

class Solution {
public:int findUnsortedSubarray(vector<int>& nums) {// 拷贝一份 numsvector<int> vec(nums);sort(vec.begin(), vec.end());int left = 0;while (left < nums.size()) {if (vec[left] != nums[left]) {break;}left++;}if (left == nums.size()) {return 0;}int right = nums.size() - 1;while (right >= 0) {if (vec[right] != nums[right]) {break;}right--;}return right + 1 - left;}
};

时间复杂度：由排序产生，O(nlogn)
空间复杂度：由拷贝的子数组产生，O(n)

参考了官方解析的做法：https://leetcode.cn/problems/shortest-unsorted-continuous-subarray/solutions/911677/zui-duan-wu-xu-lian-xu-zi-shu-zu-by-leet-yhlf/

中间数组的最大值，一定小于等于右边数组的最小值
中间数组的最小值，一定大于等于左边数组的最大值

因此，我们只需要找到，左右两边的守门员，二者相减就可以了。

class Solution {
public:int findUnsortedSubarray(vector<int>& nums) {int maxVal = -0x3f3f3f3f;int right = -1;for (int i = 0; i < nums.size(); i++) {if (nums[i] < maxVal) {right = i;}else {maxVal = nums[i];}}if (right == -1) return 0;int minVal = 0x3f3f3f3f;int left = -1;for (int i = nums.size() - 1; i >= 0; i--) {if (nums[i] > minVal) {left = i;}else {minVal = nums[i];}}return right + 1 - left;}
};

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

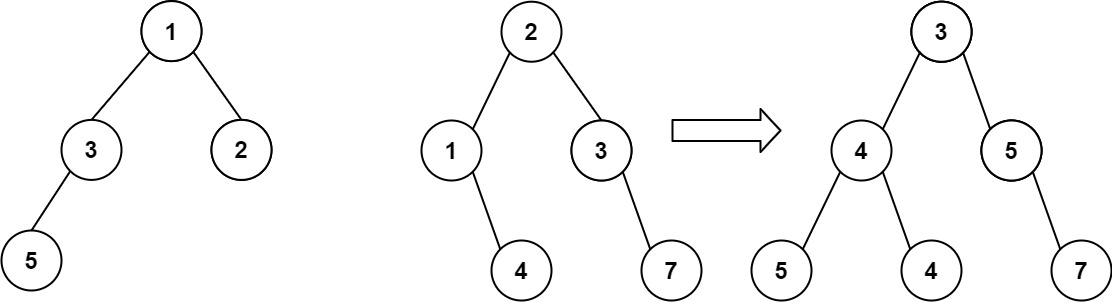
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

两棵树中的节点数目在范围 [0, 2000] 内
$-10^4<=Node.val<=10^4$

根据root1和root2是否为nullptr构建当前节点node，然后构建node->left和node->right，最后返回node。

#include<iostream>using namespace std;
// Definition for a binary tree node.
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {TreeNode* node = new TreeNode;if (root1 != nullptr && root2 != nullptr) {node->val = root1->val + root2->val;node->left = mergeTrees(root1->left, root2->left);node->right = mergeTrees(root1->right, root2->right);}else if (root1 != nullptr) {node->val = root1->val;node->left = mergeTrees(root1->left, nullptr);node->right = mergeTrees(root1->right, nullptr);}else if (root2 != nullptr) {node->val = root2->val;node->left = mergeTrees(nullptr, root2->left);node->right = mergeTrees(nullptr, root2->right);}else {delete node;node = nullptr;return node;}return node;}
};int main() {TreeNode* root1 = new TreeNode(1);root1->left = new TreeNode(3);root1->right = new TreeNode(2);root1->left->left = new TreeNode(5);TreeNode* root2 = new TreeNode(2);root2->left = new TreeNode(1);root2->right = new TreeNode(3);root2->left->right = new TreeNode(4);root2->right->right = new TreeNode(7);Solution sol;TreeNode* root = sol.mergeTrees(root1, root2);return 0;
}

621. 任务调度器

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 1：

输入：tasks = [“A”,“A”,“A”,“B”,“B”,“B”], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。

示例 2：

输入：tasks = [“A”,“A”,“A”,“B”,“B”,“B”], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
[“A”,“A”,“A”,“B”,“B”,“B”]
[“A”,“B”,“A”,“B”,“A”,“B”]
[“B”,“B”,“B”,“A”,“A”,“A”]
…
诸如此类

示例 3：

输入：tasks = [“A”,“A”,“A”,“A”,“A”,“A”,“B”,“C”,“D”,“E”,“F”,“G”], n = 2
输出：16
解释：一种可能的解决方案是：
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

提示：

$1<=task.length<=10^4$
tasks[i] 是大写英文字母
n 的取值范围为 [0, 100]

参考题解：https://leetcode.cn/problems/task-scheduler/solutions/196302/tong-zi-by-popopop/

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;class Solution {
public:int leastInterval(vector<char>& tasks, int n) {int len = tasks.size();vector<int> vec(26);for (int i = 0; i < tasks.size(); i++) {vec[tasks[i] - 'A']++;}sort(vec.begin(), vec.end(), [](int& x, int& y) {return x > y; });int cnt = 1;while (cnt < vec.size() && vec[cnt] == vec[0]) cnt++;return max(len, cnt + (n + 1) * (vec[0] - 1));}
};int main() {vector<char> tasks = { 'A','A','A','B','B','B' };Solution sol;int res = sol.leastInterval(tasks, 2);cout << res << endl;return 0;
}

647. 回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：s = “abc”
输出：3
解释：三个回文子串: “a”, “b”, “c”

示例 2：

输入：s = “aaa”
输出：6
解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

提示：

1 <= s.length <= 1000
s 由小写英文字母组成

经典动态规划题目，可以一个二维数组 dp 利用进行求解。

状态转移方程为：

if (len == 2) {dp[i][j] = (s[i] == s[j]);
}
else {dp[i][j] = dp[i + 1][j - 1] && (s[i] == s[j]);
}

代码入下：

#include<vector>
#include<string>
#include<iostream>using namespace std;class Solution {
public:int countSubstrings(string s) {int num = s.size();vector<vector<bool>> dp(num, vector<bool>(num));for (int i = 0; i < num; i++) {dp[i][i] = true;}int res = num;for (int len = 2; len <= num; len++) {for (int i = 0; i < num - len + 1; i++) {int j = i + len - 1;if (len == 2) {dp[i][j] = (s[i] == s[j]);}else {dp[i][j] = dp[i + 1][j - 1] && (s[i] == s[j]);}if (dp[i][j] == true) res++;}}return res;}
};int main() {string s = "aaaaa";Solution sol;int res = sol.countSubstrings(s);cout << res;
}