💞💞 前言
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:大耳朵土土垚的博客
💥 所属专栏:数据结构学习笔记
💥对于数据结构顺序表、链表、堆有疑问的都可以在上面数据结构的专栏进行学习哦~ 有问题可以写在评论区或者私信我哦~
前面我们学习过二叉树的前、中、后序遍历 以及二叉树层序遍历,今天我们将继续学习有关二叉树的实现🥳🥳🥳
1.二叉树的构建
1.1二叉树的结构
typedef char BTDataType;//这里使用字符类型方便看下面的ABC等字母
//typedef int BTDataType;其他我们使用int
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//二叉树的结构二叉树每个节点应该包含该节点的值,以及其左右子节点的地址
1.2创建二叉树新节点
//创建新节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");return NULL;}newnode->data = x;return newnode;
}
使用malloc函数创建节点,最后销毁时要使用free来释放,malloc大小为BTNode的节点;
对于mallc函数有疑问的可以查看土土的博客——动态内存函数介绍;
1.3创建二叉树
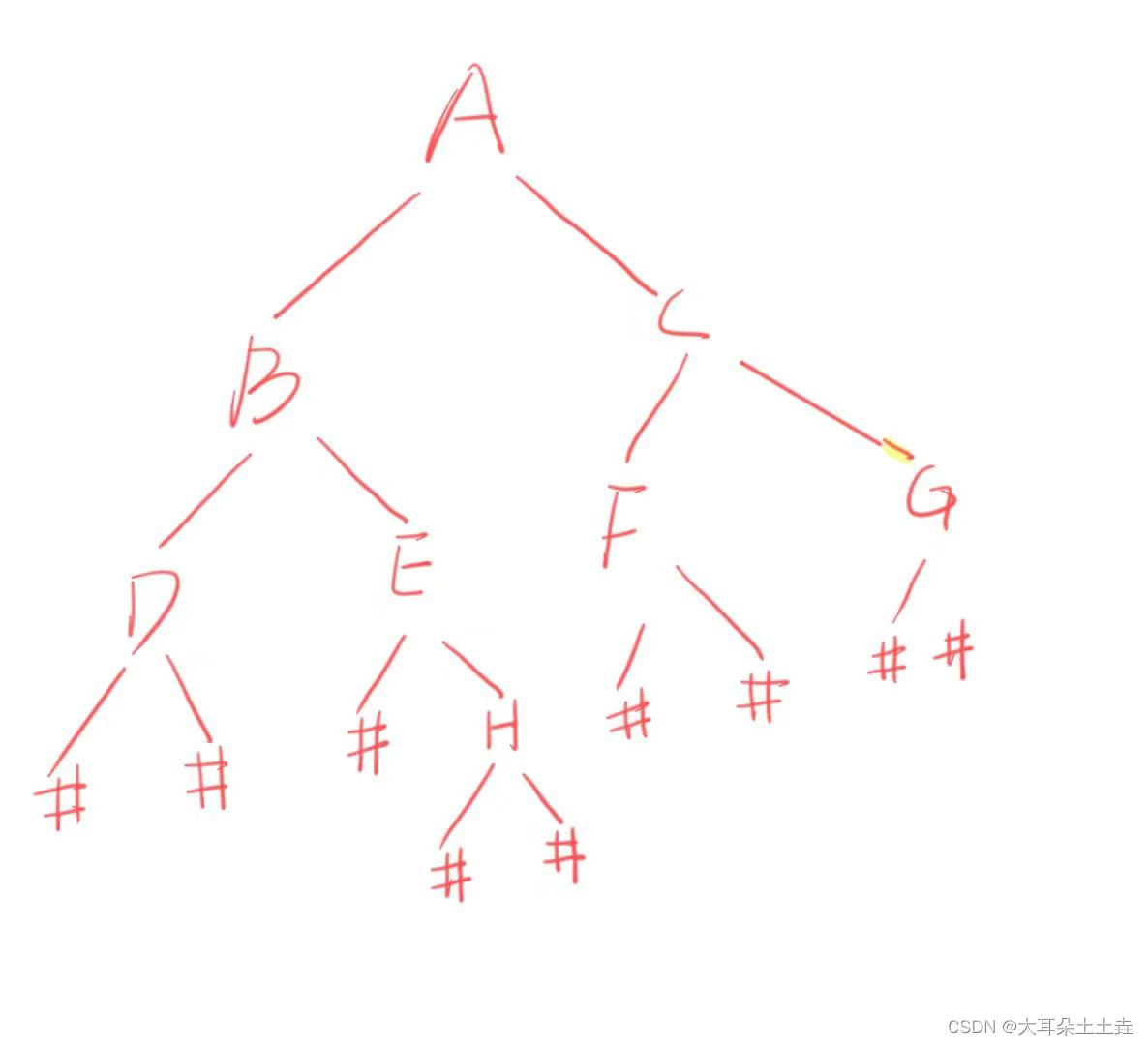
以数组"ABD##E#H##CF##G##"为例
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{if(a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BuyNode(a[*pi]);(*pi)++;root->left = BinaryTreeCreate(a, pi);root->right = BinaryTreeCreate(a, pi);return root;
}
利用监视进行可视化如下:

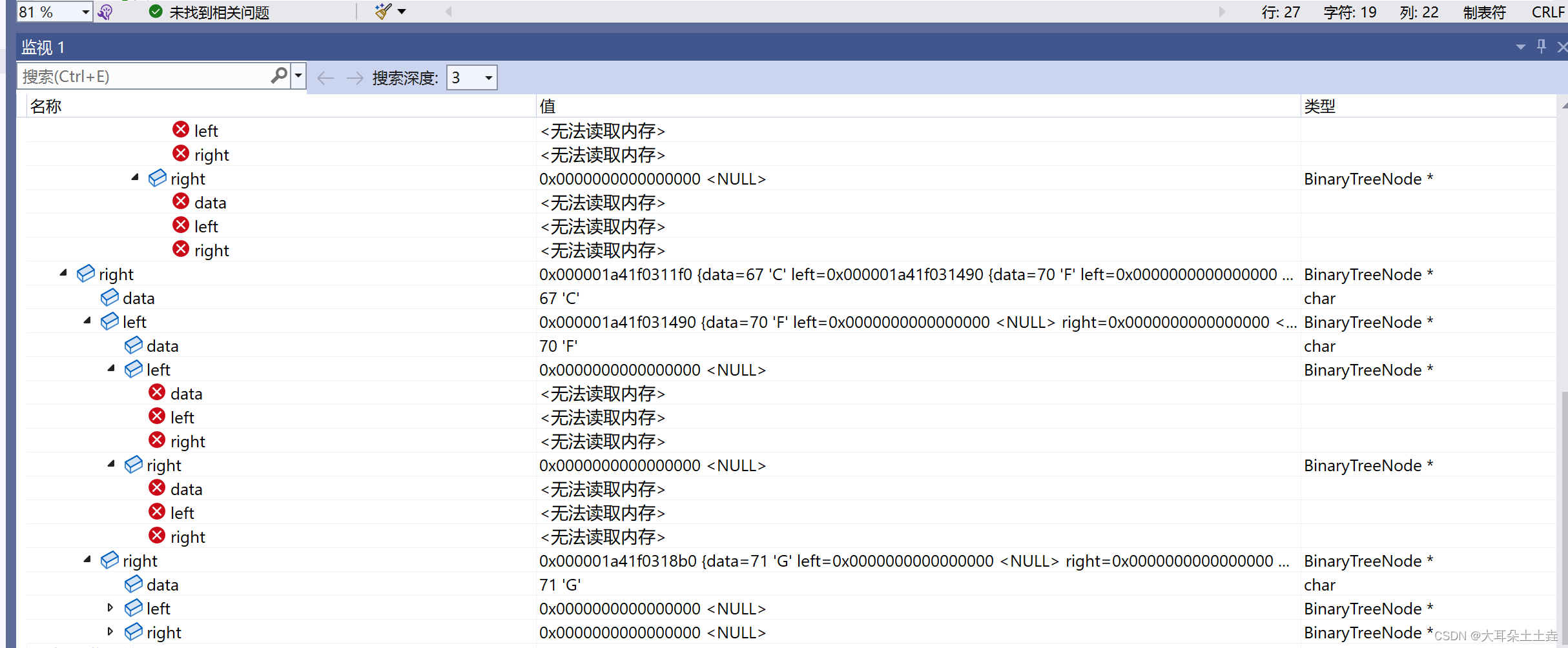
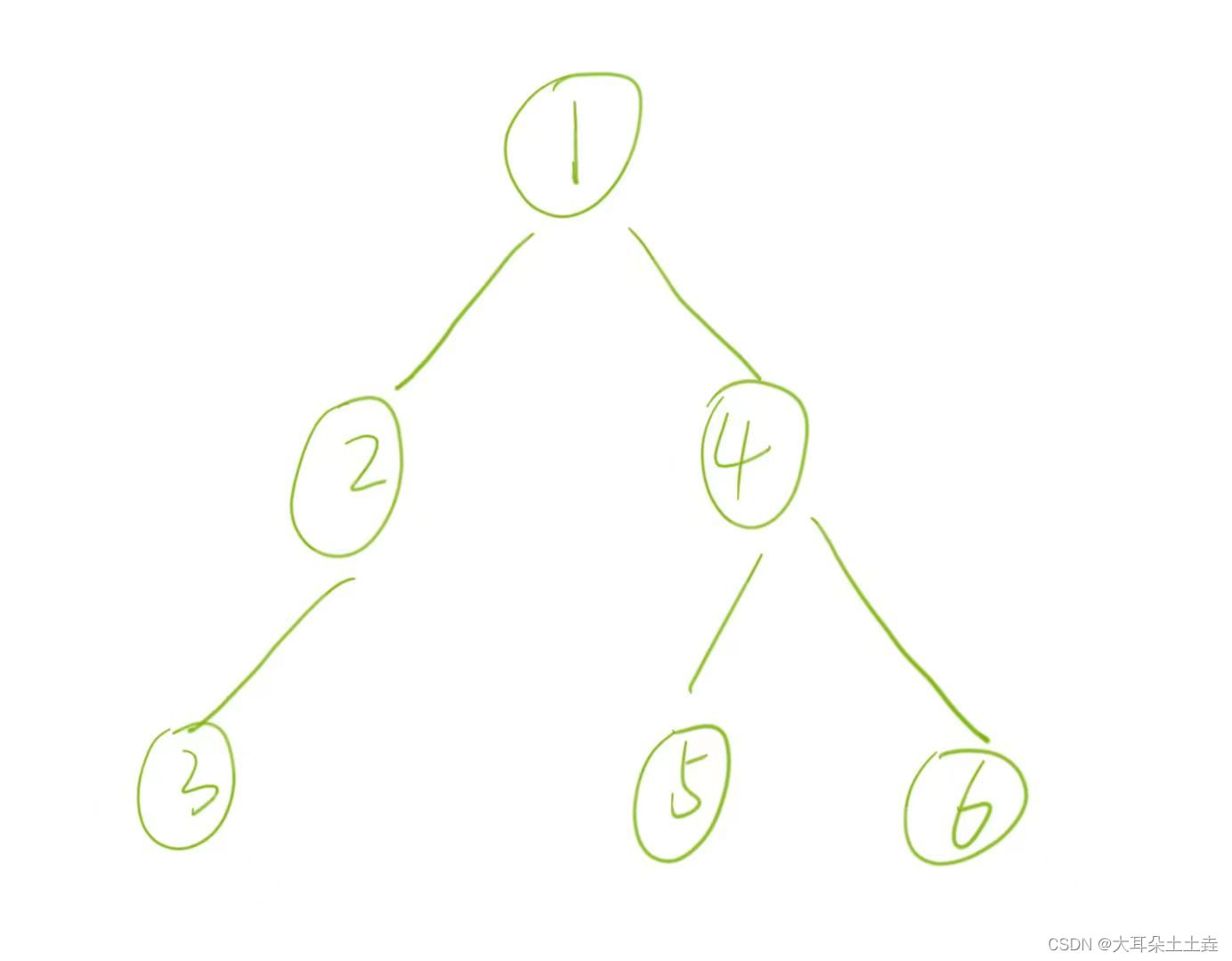
可以看到形成了逻辑结构如下图所示的二叉树:
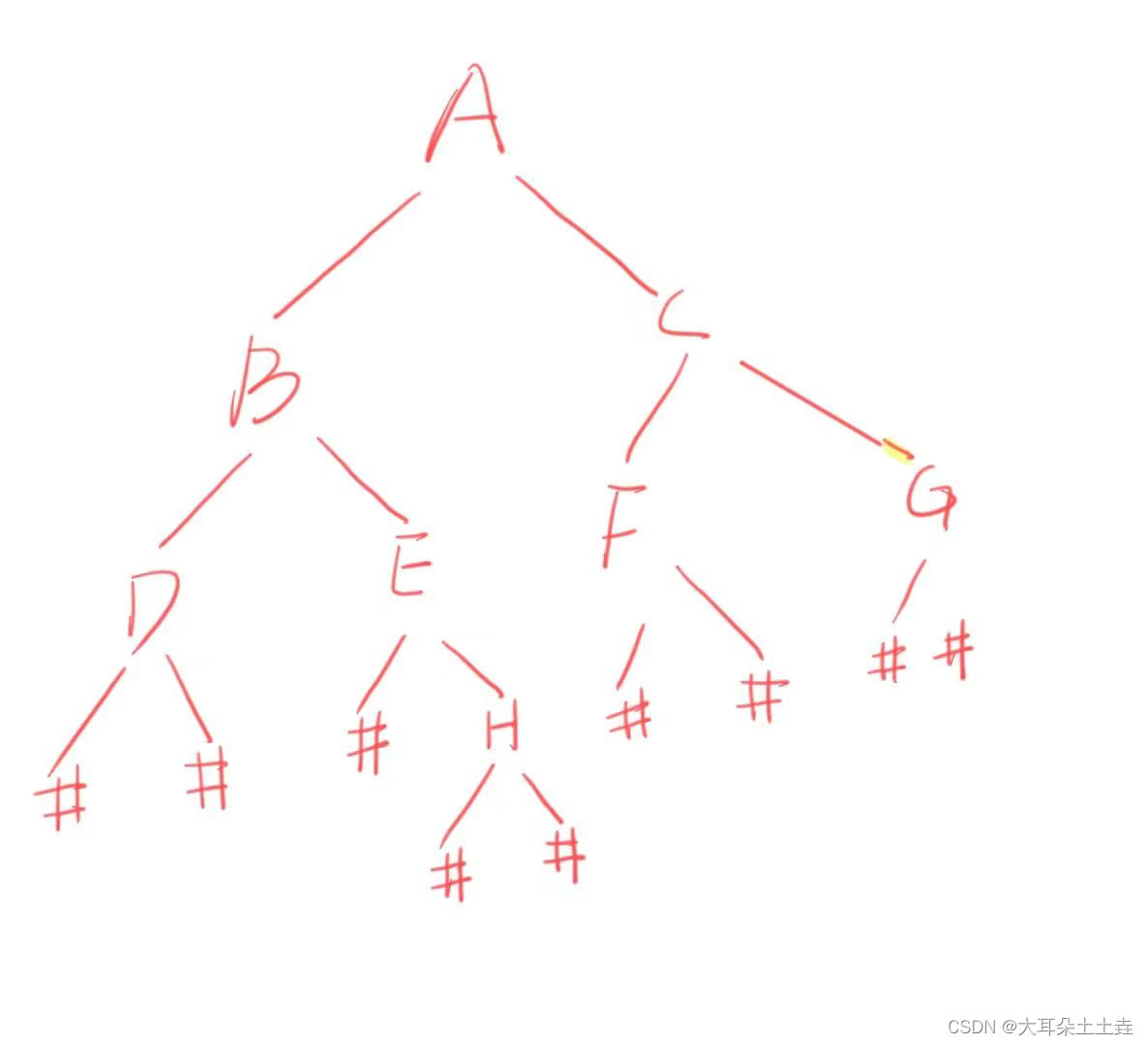
我们将这里的’#'当作空的标志,用来实现二叉树的结构,并利用递归左子树右子树来构建二叉树。
2.二叉树的销毁
// 二叉树销毁
void BinaryTreeDestroy(BTNode* root)
{if (root == NULL)return;//类似于后序,先释放左右子树再释放根节点BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);
}
这里二叉树的销毁需要对二叉树进行遍历,我们前面学习过四种二叉树的遍历——前、中、后序以及层序遍历,对于销毁二叉树来说使用后序遍历比较合适,因为先释放左右子树再释放根节点这样可以防止找不到节点。
3.二叉树节点个数
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{/*if (root == NULL)return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;*/return root == NULL ? 0 : BinaryTreeSize(root->left)+ BinaryTreeSize(root->right) + 1;
}
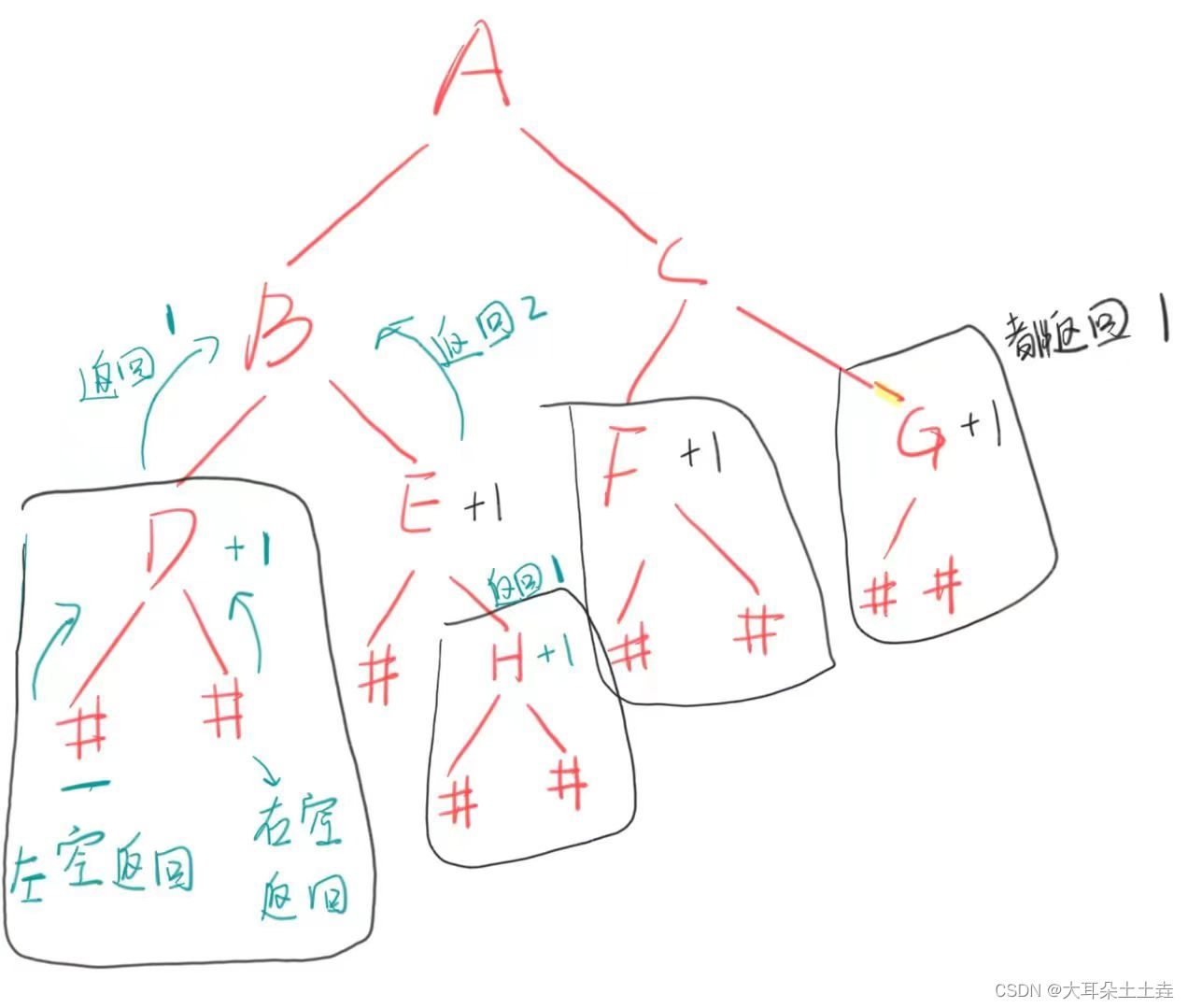
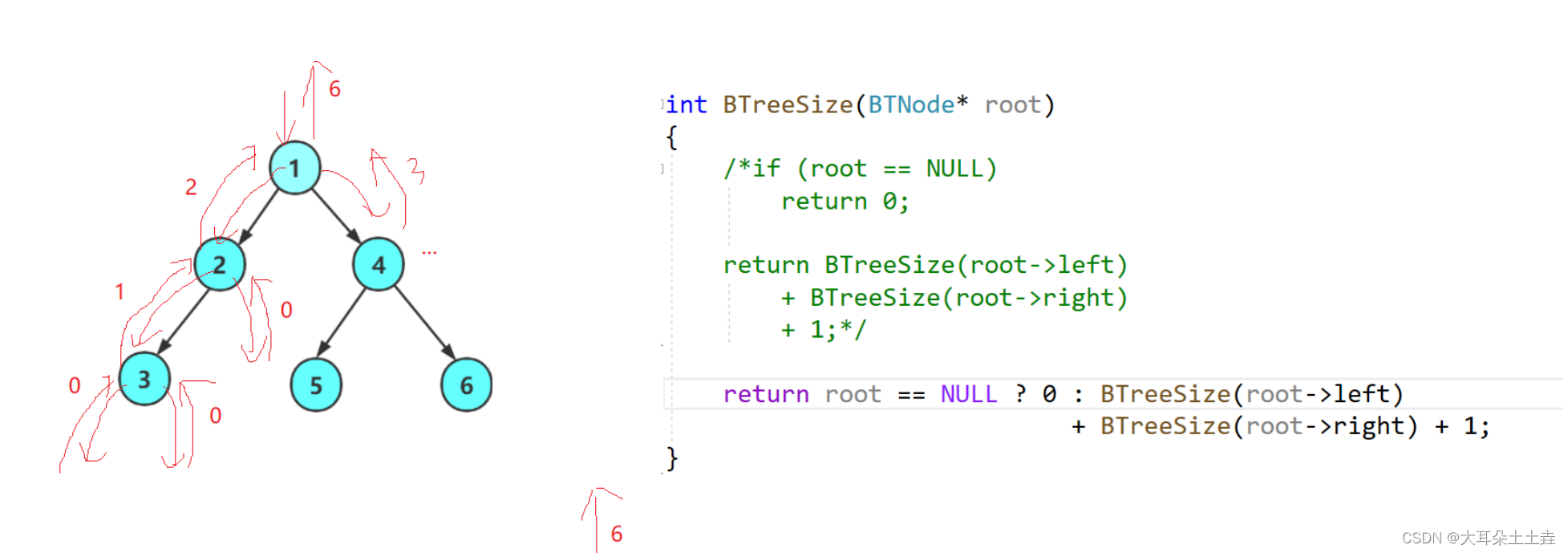
如果节点是空就返回,不是空就继续递归找其左子树右子树直到找到空也就是叶子节点的左右子树,此时再递归返回叶子节点的父节点时要+1,用来表示计算的叶子节点;依次类推不是NULL就+1,这样最后就是二叉树节点的个数了;图解如下:
以下图为例:
1.找到NULL:
返回左右子树为空后要+1;
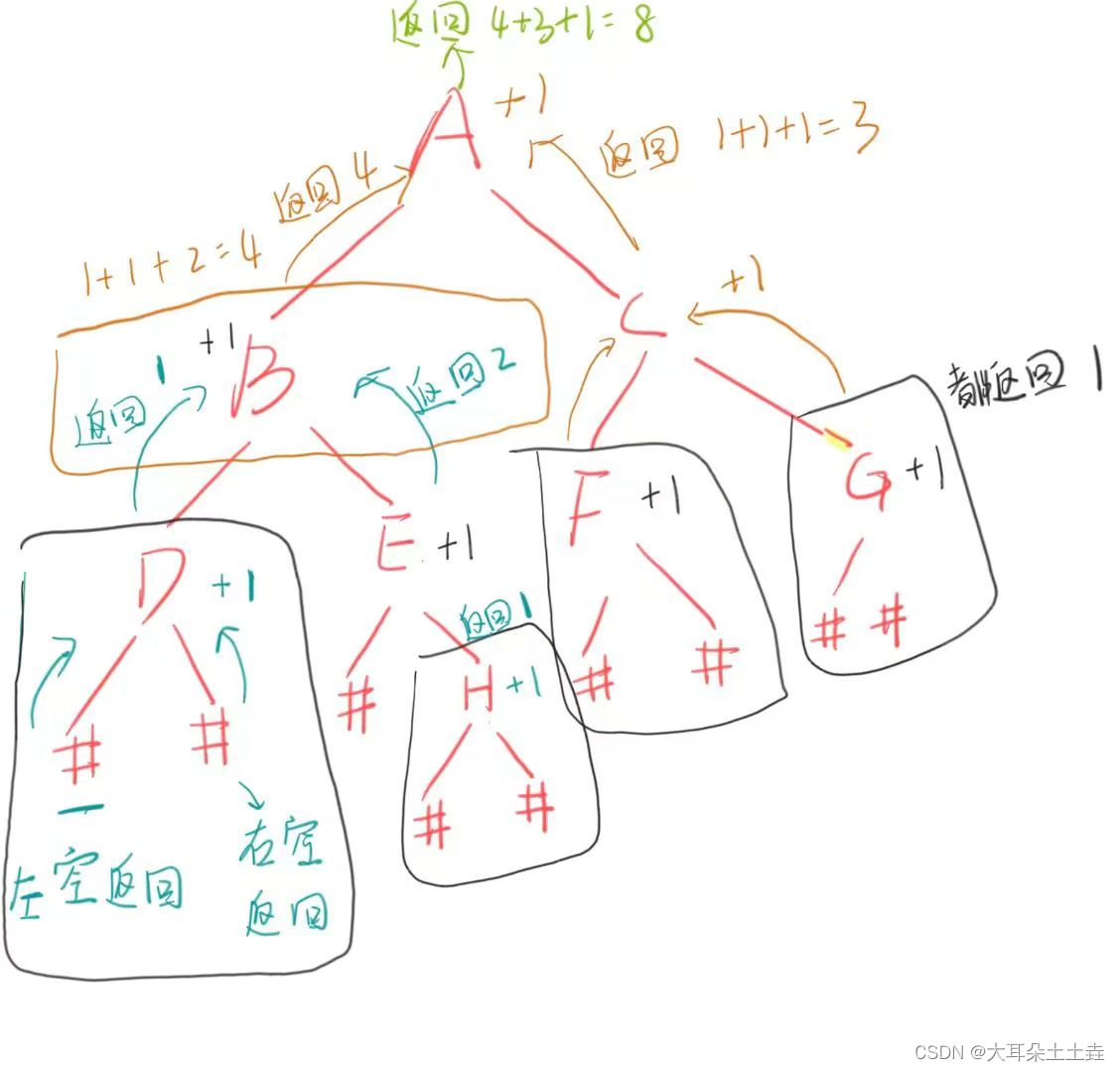
2.依次类推递归返回:
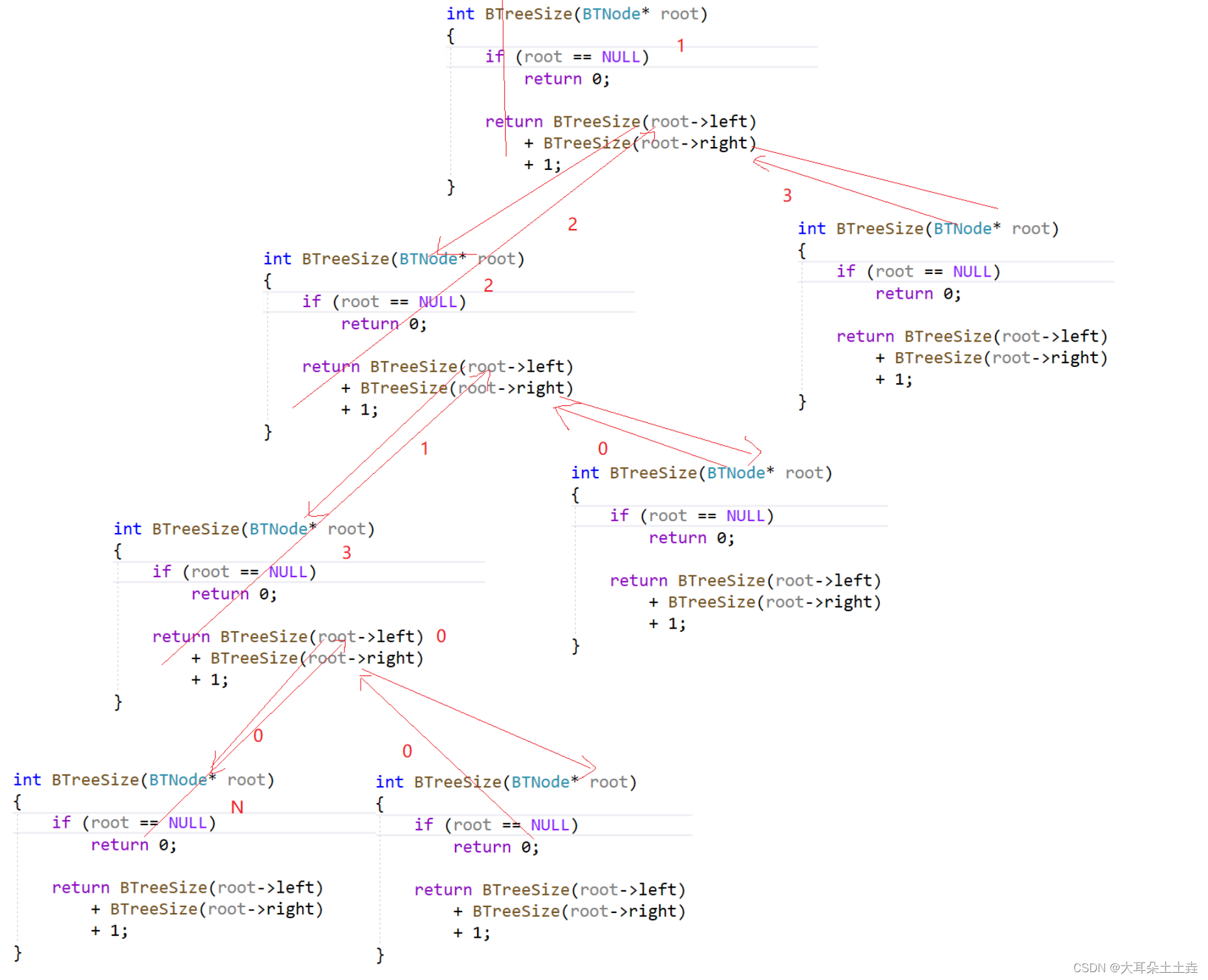
也可以看下面的递归展开图:
以下图为例:
4.二叉树叶子节点个数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;//叶子节点if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
叶子节点对应其左右子树都为空,就返回1,利用递归实现
5.二叉树第k层节点个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k);if(root == NULL)return 0;//k层节点个数if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
我们可以利用k-1依次往下递归,直到k = 1 时此时,就是第k层就返回1;
6.二叉树查找
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//前序遍历来查找if (root->data == x){return root;}BTNode* res1 = BinaryTreeFind(root->left, x);if (res1)return res1;BTNode* res2 = BinaryTreeFind(root->right, x);if (res2)return res2;//没有找到返回空return NULL;
}
在运用递归时要返回值时记得将递归找到的值保存起来,防止找不到耗费力气重新再找。
7.二叉树高度
//求二叉树高度
int BTreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = BTreeHeight(root->left);int rightHeight = BTreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
类似于二叉树节点个数的递归,返回时每次+1,并且我们还需要将每次计算的高度与二叉树查找一样保存起来防止浪费时间再去遍历查找,此外左子树右子树高度不一致时要取较大的那一个;
8.判断是否是完全二叉树
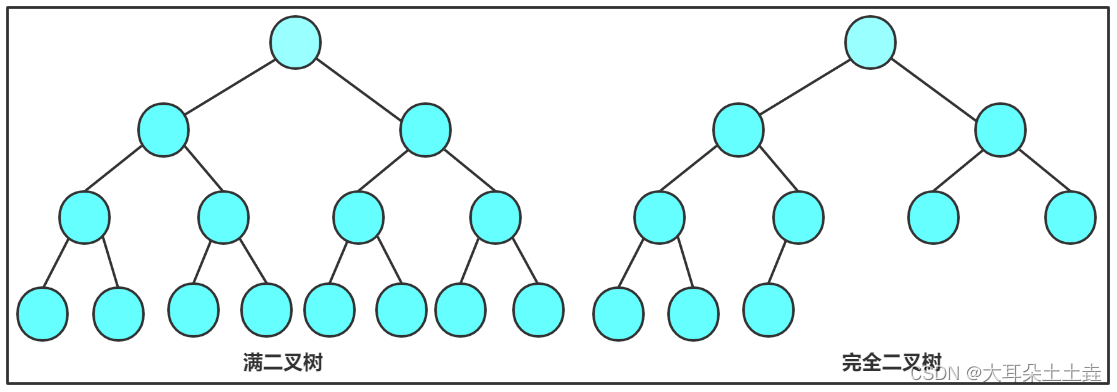
在此之前我们先回顾一下特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k - 1 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
要注意的是满二叉树是一种特殊的完全二叉树。
这里判断是否为完全二叉树的实现与之前讲过的二叉树层序遍历相似需要利用队列来实现,队列的实现在这——二叉树层序遍历里面包含队列代码的完整实现,这里就不过多描述,我们直接来使用。记得使用时要先写队列并包含对应的头文件哦~
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{//利用队列先进先出的特点Queue qt;QueueInit(&qt);if (root)//如果根节点非空则入队列QueuePush(&qt, root);while (!QueueEmpty(&qt))//判断队列非空{QDataType front = QueueFront(&qt);//取出队头元素QueuePop(&qt);if (front == NULL)break;//遇到空就跳出QueuePush(&qt, front->left);//再将左右子树的节点入队列QueuePush(&qt, front->right);}//break跳出后//判断之后的元素是否有非空值//有非空值则不是完全二叉树while (!QueueEmpty(&qt)){QDataType front = QueueFront(&qt);QueuePop(&qt);if (front != NULL){QueueDestroy(&qt);return false;}}//如果没有非空值返回trueQueueDestroy(&qt);return true;
}
思路:利用二叉树的层序遍历,层序遍历一遍如果有空指针NULL且队列非空时如果队列里面还有非空值那么就不是完全二叉树。
9.结语
以上就是有关二叉树实现的内容啦 ~ 关键是要理解递归是怎么实现的,利用二叉树由根节点、左右子树构成的特性来实现递归,完结撒花 ~🥳🥳🎉🎉🎉