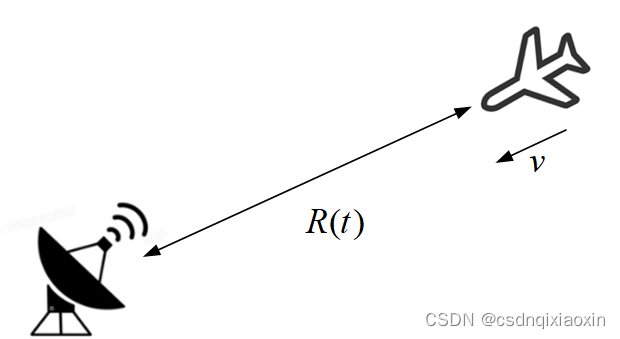
下面从频谱的角度理解多普勒频移。

---

设目标以速度接近雷达，在时刻距离，则在任意时刻目标与雷达的距离为

设雷达发射信号为。设时刻发射的信号经过遇到目标，则由于目标与信号相向运动，有

得到，从而时刻发射的信号经过返回雷达，所以接收信号为

将带入得

其中。

可以看到，接收信号是发射信号在时域的压缩。根据傅里叶变换的性质，接收信号的频谱是发射信号频谱的展宽。也就是说，假设的频谱是，则有：

---

下面推导常用的带通信号的频谱。设发射信号，它的频谱即傅里叶变换为

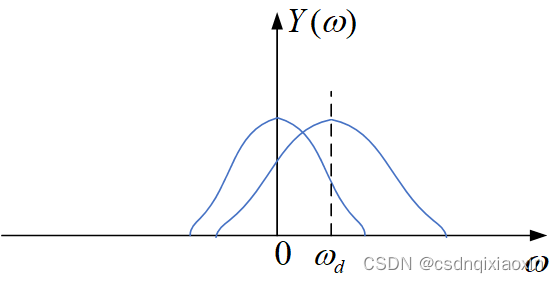
设如下图所示，注意这里画的实际上是频谱幅度：

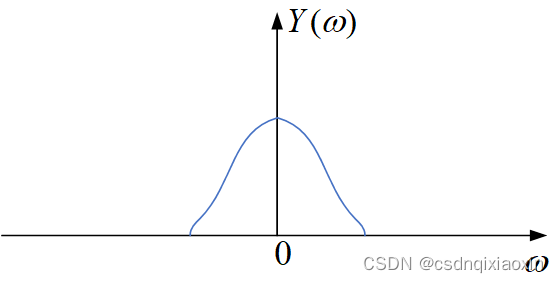
则相当于将搬移到的位置：

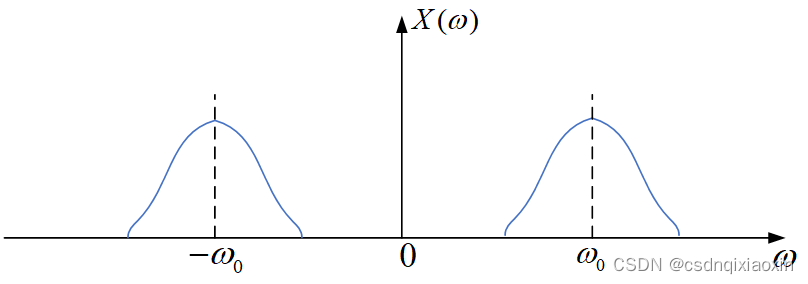
而接收信号为

现在忽略的影响（是一个固定的时延，频谱上则对应于一个移相），则

从而接收信号的频谱为

可以看到，是对沿横轴展宽倍，再搬移到的位置：

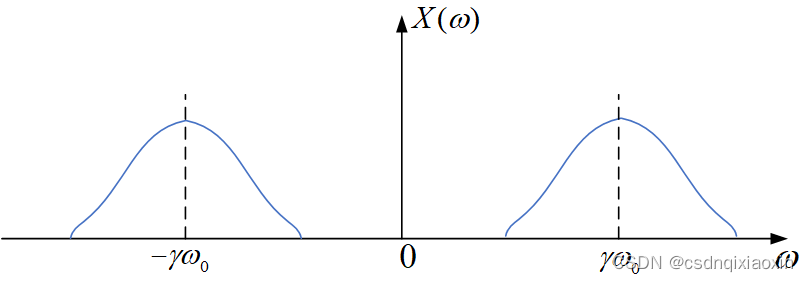
多普勒频率则定义为中心频率的偏移：

写成频率形式：

将接收信号变到基带，对比下多普勒频率为0和不为0的频谱：