-
背景知识
-
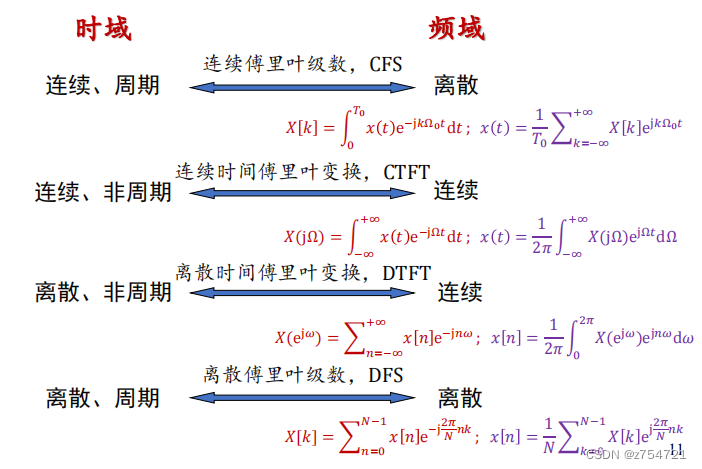
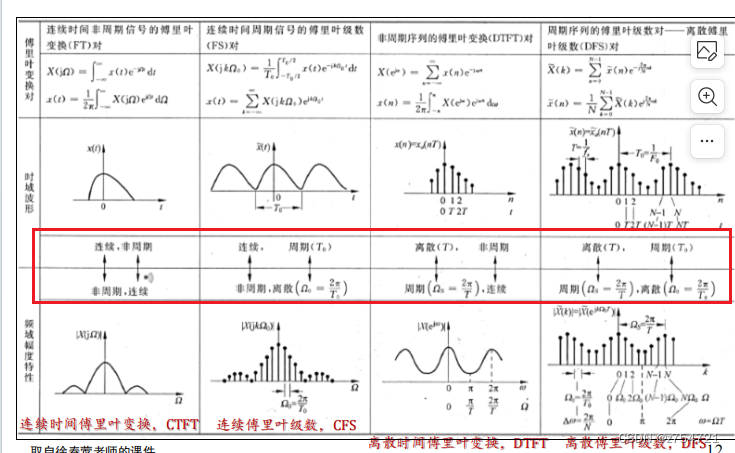
四种基本的傅里叶变换
-
基本思想:将信号表示为不同频率 正弦分量的线性组合
-
正弦信号和复指数时间信号的有用特性
-
相同频率但不同相位的正弦信号的任何线性组合,都是有着相同频率但不同相位,且幅度可能受改变的正弦信号。
-
复指数时间信号不同延迟版本的任何线性组合,等于该信号乘以一个复系数,由复系数决定其幅度和相位的变化。
-
-
四种常用的傅里叶变换
-
-
-
-
离散傅里叶变换
-
DFT的定义
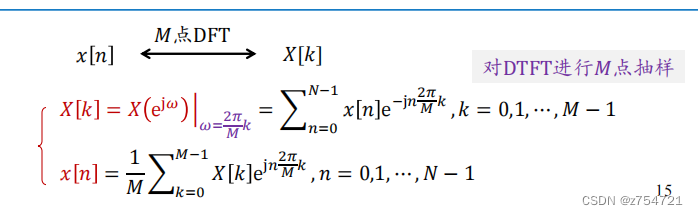
-
频域抽样的分析:
-
时域抽样导致频域上的周期延拓
-
频域抽样导致时域上的周期延拓
-
-
-
DFT的重要性质
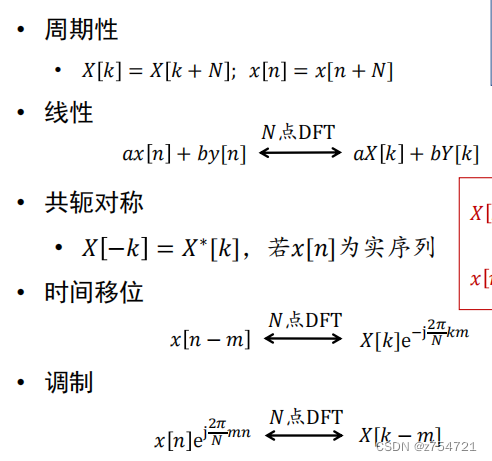
-
DFT的高效实现:FFT
-
比较:直接计算DFT:对于每个𝑘,需要𝑁次复数乘法和𝑁 − 1次复数加法操作;因而总共需要大约𝑁²次操作,利用DFT的快速实现算法:只需要大约𝑁 log2 𝑁 次操作。
-
基本思想:递归地将较长序列的DFT分解为较短序列的DFT
-
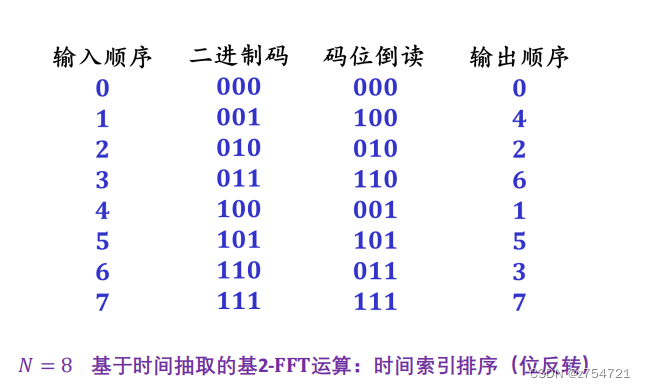
例子:
-
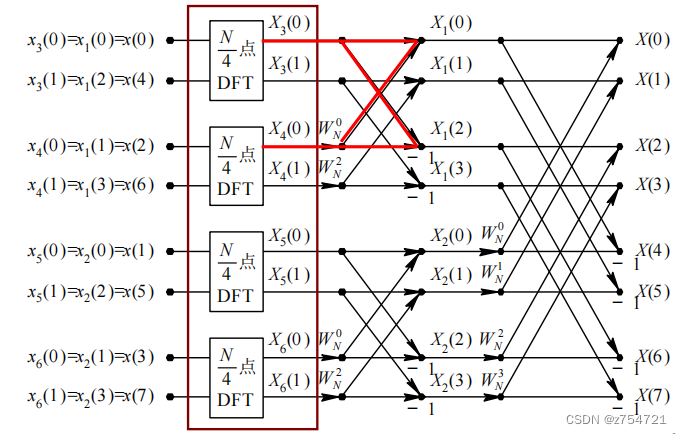
-
 计算IDFT:对X[k]进行共轭,然后进行DFT得到再除以n,得到x[n[的共轭,然后取反共轭即可。
计算IDFT:对X[k]进行共轭,然后进行DFT得到再除以n,得到x[n[的共轭,然后取反共轭即可。
-
-
-
DFT的应用
-
频谱分析(使用DFT对连续时间信号的频率成分进行数值分析)
-
步骤:
-
• 第1步:时域抽样(Sample in time),抽样频率𝑓s
-
• 第2步:时域截短(Truncate in time),加窗
-

-
频谱泄露与频率分辨率的例子:

-
-
• 第3步:频域抽样(Sample in frequency),求𝑵点DFT
-
-
-
线性卷积(利用DFT来完成卷积的思路):
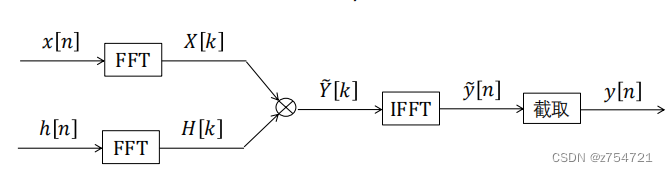
-
-
从矩阵观点看DFT和FFT
频率分析和离散傅里叶变换——DSP学习笔记四
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/314465.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
软件物料清单(SBOM)生成指南 .pdf
如今软件安全攻击技术手段不断升级,攻击数量显著增长。尤其是针对软件供应链的安全攻击,具有高隐秘性、追溯难的特点,对企业软件安全威胁极大。
同时,软件本身也在不断地更新迭代,软件内部成分安全性在持续变化浮动。…
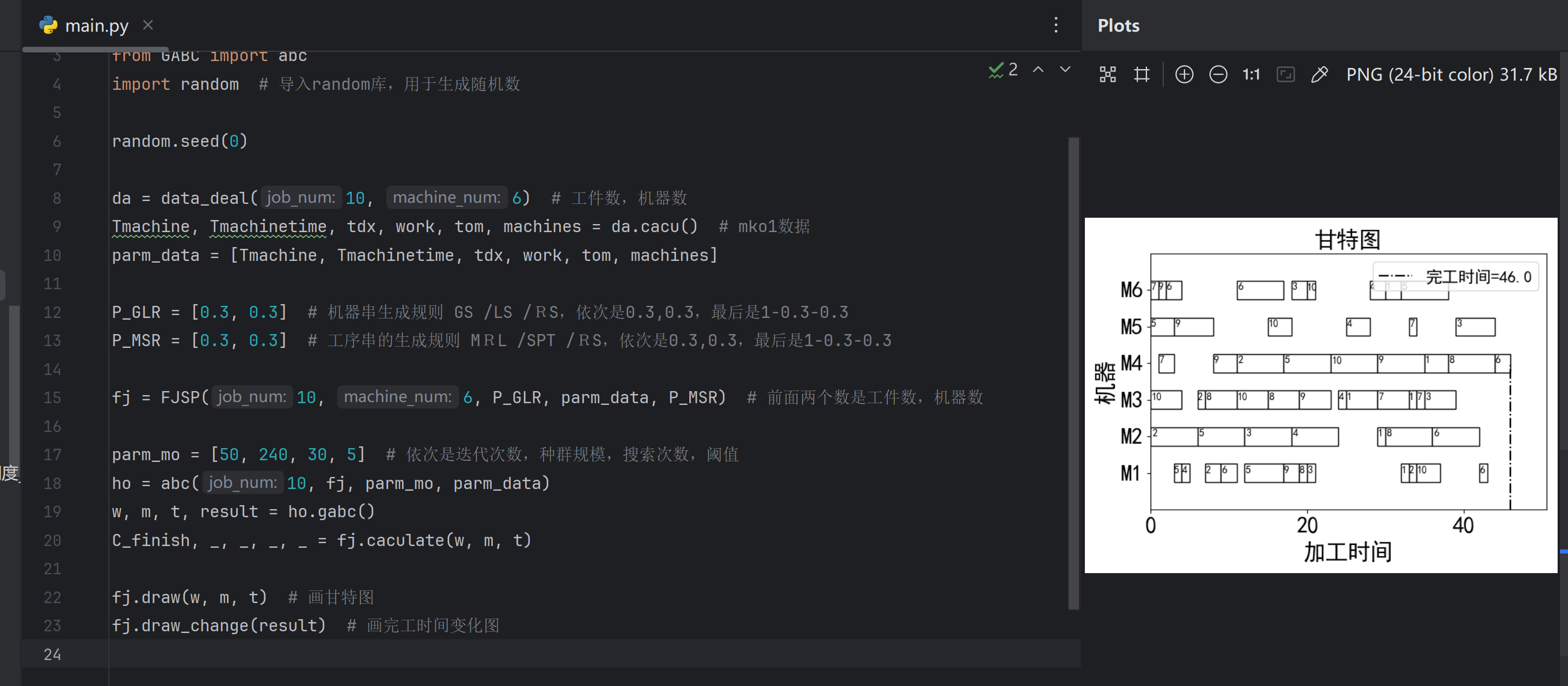
【算法】人工蜂群算法,解决多目标车间调度问题,柔性车间调度问题
文章目录 复现论文什么是柔性作业车间调度问题?数据处理ABC算法编码解码种群初始化雇佣蜂操作IPOX交叉多点交叉 观察蜂操作侦察蜂操作算法流程 结果程序截图问询、帮助 复现论文 什么是柔性作业车间调度问题?
也叫多目标车间调度问题。
柔性作业车间调…
为什么有的晶圆厂叫特色工艺晶圆厂?
知识星球(星球名:
芯片制造与封测社区)里的学员问:
经常看看到某某晶圆厂是12英寸特色工艺晶圆厂,特色工艺是指什么? 芯片的种类?
芯片分为四大类:mems,IC,光电器件,分立器件。
…
web(微博发布案例)
示例:
1、检测空白内容 2、发布内容 html:
<!DOCTYPE html>
<html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta …
科蓝尔环保 | 成都2024全国水科技大会暨技术装备成果展览会
2024年5月13日一15日中华环保联合会、福州大学、上海大学在四川省成都市联合举办“2024全国水科技大会暨技术装备成果展览会”。
大会主题:加快形成新质生产力 增强水业发展新动能
大会亮点:邀请6位院士,100余位行业专家,15场专…
Redis缓存问题:穿透,击穿,雪崩等
Redis缓存问题:穿透,击穿,雪崩等
在高并发场景下,数据库往往是最薄弱的环节,我们通常选择使用redis来进行缓存,以起到缓冲作用,来降低数据库的压力,但是一旦缓存出现问题,也会导致数据库瞬间压力过大甚至崩溃,从而导致整个系统崩溃.今天就聊聊常见的redis缓存问题.
缓存击穿 …
了解HTTP代理服务器:优势、分类及应用实践
在我们日常的网络使用中,我们经常听到HTTP代理服务器这个术语。那么,HTTP代理服务器到底是什么?它有什么优势和分类?又如何应用于实践中呢?让我们一起来了解一下。
HTTP代理服务器是一种位于客户端和服务器之间的中间…
qml和c++结合使用
目录 文章简介1. 创建qml工程2. 创建一个类和qml文件,修改main函数3. 函数说明:4. qml 文件间的调用5. 界面布局6. 代码举例 文章简介
初学qml用来记录qml的学习过程,方便后面归纳总结整理。
1. 创建qml工程
如下图,我使用的是…
数字IC后端先进工艺设计实现之TSMC 12nm 6Track工艺数字IC后端实现重点难点盘点
大家知道咱们社区近期TSMC 12nm ARM Cortexa-A72(1P9M 6Track Metal Stack)已经开班。这里小编要强调一点:不要认为跑了先进工艺的项目就会很有竞争力!如果你仅仅是跑个先进工艺的flow,不懂先进工艺在数字IC后端实现上的不同点,为何有这样的不…
【笔记】应对Chrome更新导致Chromedriver失效的解决方案:Chrome For Test
随着网络应用和网站的不断发展,自动化测试变得越来越重要,而Selenium成为了许多开发者和测试人员的首选工具之一。然而,对于使用Selenium来进行网站测试的人来说,Chrome浏览器的频繁更新可能会成为一个头疼的问题。每当Chrome更新…
论文速览 | IEEE TIFS, 2021 | 对车载毫米波雷达的物理层攻击及其防御方法的研究
注1:本文系"计算成像最新论文速览"系列之一,致力于简洁清晰地介绍、解读非视距成像领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; CVPR, ICCV, ECCV, SIGGRAPH, TPAMI; Light‑Science & Applications, Optica 等)。 本次介绍的论文是:<2…
iOS——NSCache
什么是NSCache
NSCache是Foundation框架中的一个类,用于在iOS和macOS应用程序中进行临时性的内存缓存。它提供了一种轻量级的缓存机制,可以用于存储临时性的数据,例如图片、对象等。NSCache的主要特点和用法包括: 临时性缓存&…
汽车纵染压制专用液压机比例阀放大器
汽车纵染压制专用液压机比例阀放大器是一种专门用于汽车纵梁拉伸工艺的设备,它也可以用于其他金属薄板的压制成型及校正工艺。该类型的液压机通常具备独立的动力机构和电气系统,采用PLC技术进行控制,以确保操作的准确性和稳定性。除了纵梁拉伸…
openEuler-22.03安装redis6.2.7
前言:redis一开始是安装5.0.7,一直安装失败
gcc安装版本是 10.3.1 make报错 参考博客:https://blog.51cto.com/flyfish225/10596050
将redis版本换成 6.2.7
1、下载地址
https://download.redis.io/releases/redis-6.2.7.tar.gz
2、解压…
OpenHarmony硬件合成方案解析
本文档主要讲解在OpenHarmony中,硬件合成适配的方法及原理说明。
环境说明:
OHOS版本:3.1-Release及以上
一、背景介绍
1.1 什么是合成
要理解什么是合成,合成做了什么?我们先通过分解设置界面来回答这个问题: 在…
删除二叉搜索树中的节点
题目链接
删除二叉搜索树中的节点
题目描述 注意点
节点值唯一root 是合法的二叉搜索树节点数的范围 [0, 10000]
解答思路
可以根据二叉搜索树的性质找到要删除的节点,关键是删除节点后怎么重新构建成一棵新的二叉搜索树首先要找到的是删除节点node的父节点nod…
数智时代的AI人才粮仓模型解读白皮书(2024版)
来源:极客邦科技
自 2023 年上半年起,ChatGPT 等大模型技术蓬勃发展,AI 技术不断突破边界,展现 出惊人的潜力和发展速度。从早期的逻辑推理、专家系统,到如今的深度学习、神经网络, AI 技术显著缩小了科学…
【webrtc】Chrome和Firefox在SDP协商过程中,针对localhost的不同处理
内网下chrome端webrtc协商失败
现象
我有一个webrtc服务器在局域网内,使用chrome浏览器访问时,发现webrtc在做媒体协商时失败。
具体表现是,在交换sdp后,ice的状态是oniceconnectionstatechange: failed
但是换成Firefox浏览器…
编写Spark独立应用程序
执行本文之前,先搭建好spark的开发环境,我目前只搭建了standalone模式,参考链接 : Spark Standalone模式部署-CSDN博客
1. 安装sbt
1)下载sbt 网址:https://www.scala-sbt.org/download.html ,…
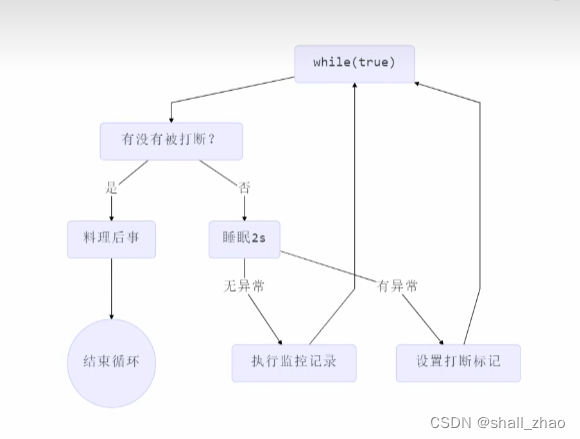
设计模式——终止模式之两阶段终止模式
文章目录 1. 错误思路2. 两阶段终止模式2.1 利用 isInterrupted2.2 利用停止标记interrupt-打断park Two Phase Termination 在一个线程 T1 中如何“优雅”终止线程 T2?这里的【优雅】指的是给 T2 一个料理后事的机会。
1. 错误思路
使用线程对象的 stop() 方法停…
推荐文章
- 营销人在酒桌上如何说话
- ChatGPT 国产平替上线;FTC 阻止微软 690 亿美元收购动视暴雪;PHP 8.2.0 发布|极客头条
- GENIUS: 根据草稿进行文本生成的预训练模型,可用于多种NLP任务的数据增强...
- HTML代码混淆技术:原理、应用和实现方法详解
- telnetlib -- Telnet 客户端
- 软考-高级-信息系统项目管理师教程 第四版【第19章-配置与变更管理-思维导图】
- 腾讯定性微信QQ故障为一级事故,总办成员遭处罚;OpenAI CEO考虑在日本开设办事处;OpenBSD 7.3发布|极客头条...
- #Css篇:实现一个元素水平和垂直居中实现左右固定,中间自身适应布局 左侧固定 右侧自适应
- #成为 SQL 大师#groupby 中不能有聚合函数
- (※)力扣刷题-字符串-实现 strStr()(KMP算法)
- (AI Web、ChatGPT Native、Ai Loading、AI Tools、知豆AI)
- (NeurIPS,2022)Knowledge-CLIP:使用知识图谱进行CLIP