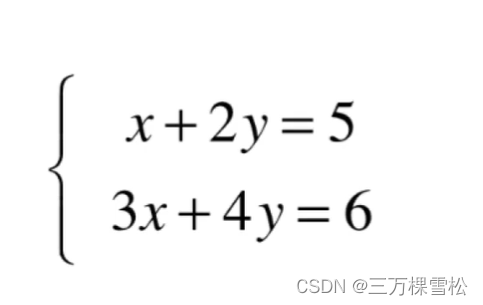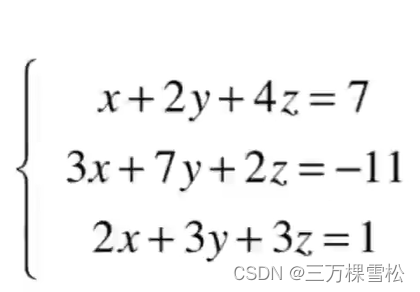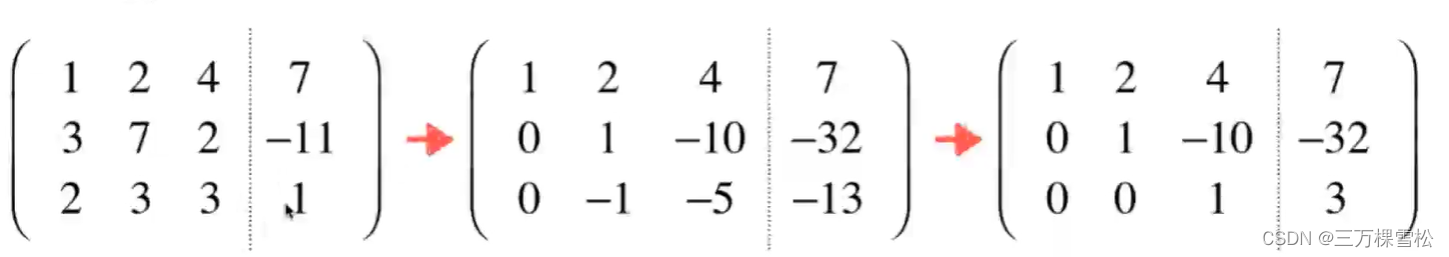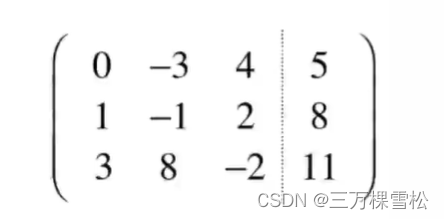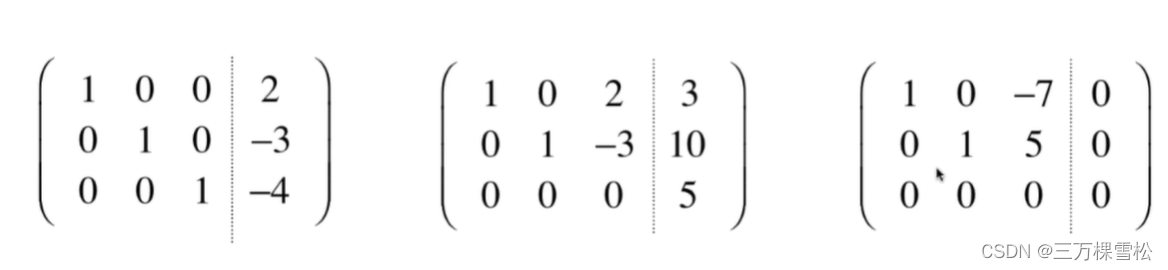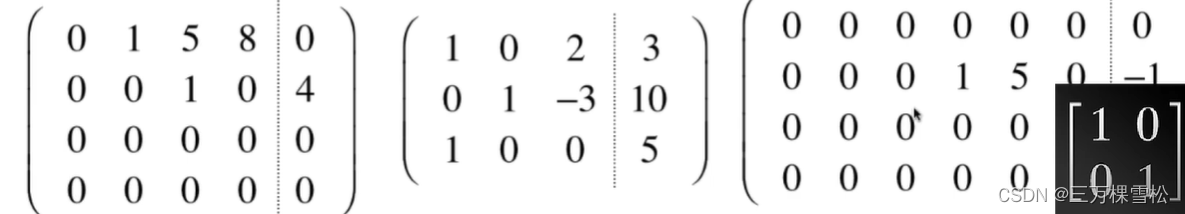线性系统(一)
- 1.什么是线性系统
- 2.高斯消元法
- 3.高斯-约旦消元法
- 4.线性方程组解的结构
链接: 线性系统(二)
1.什么是线性系统
线性:未知数只能是一次方项
非线性:
同时,读者也可以通过作图来更直观地感受(都是曲线)。
2.高斯消元法
原来的方程组
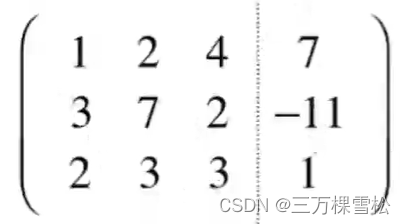
增广矩阵(在系数矩阵的基础上加上结果)
高斯消元的过程
所涉及到的操作
1.矩阵的某一行乘以一个常数
2.矩阵的一行加(减)另一行
3.交换矩阵的两行
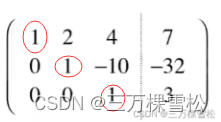
核心是把每行的主元,即下图红圈处化为1。再把主元之下化为0。
如果遇到以下情况,可以将第一行其他行换行。
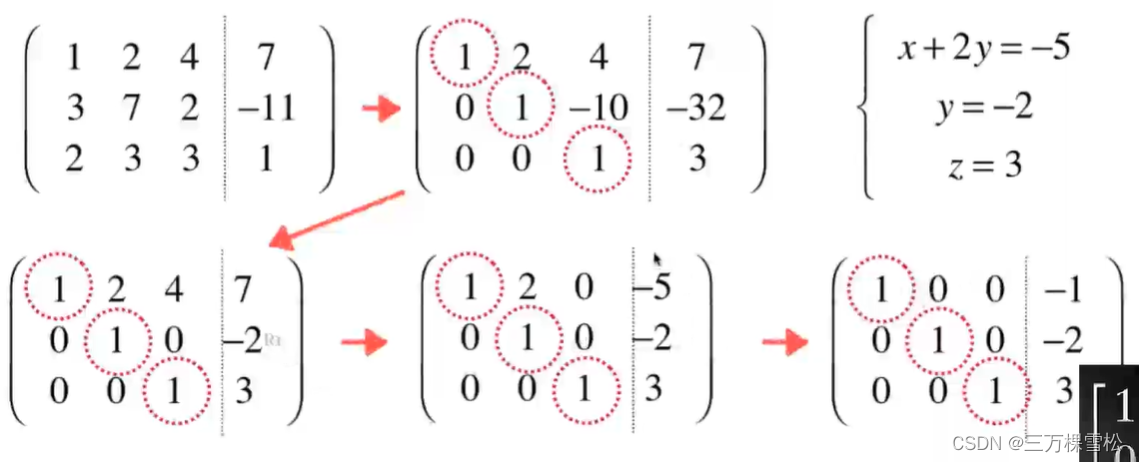
3.高斯-约旦消元法
与高斯消元法差不多,只是在前者基础上从上往下再从下往上,优化了回代的过程。
具体操作
前向过程(从上到下)
1.选择最上的主元,化为1
2.主元下面的所有行减去主元所在行的某个倍数,使得主元下面所有元素都为0
后向过程(从下到上)
1.选择最下的主元
2.主元上面的所有行减去主元所在行的某个倍数,使得主元上面所有元素都为0
4.线性方程组解的结构
第一个有唯一解 。
第二个无解,最后一行不成立
第三个有无数解。不同取值对应不同的解。
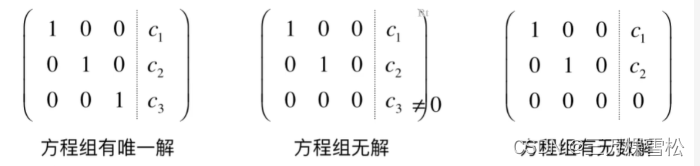
归纳一下就是
类似于这样的阶梯型矩阵,并且非零行的第一个元素(主元)为1,主元所在列的其他元素均为0。那么我们就叫此矩阵为行最简形式。
如下就不是行最简形式
第一个第一行的5应为0
第二个第三行的1不符合
第三行第一行作为全零行应在最下面