金融风控实战——有监督分箱

卡方分箱

分箱的方法有很多，卡方分箱属于其中一种，属于有监督系列的。卡方分箱正是一种基于卡方检验的分箱方法，更具地说是基于上面提到的第二种应用，独立性检验，来实现核心分箱功能的。
卡方分箱算法简单来说，有两个部分组成：1）初始化步骤；2）合并。
小栗子：

计算所有相邻分箱的卡方值：也就是说如果有1,2,3,4个分箱，那么就需要绑定相邻的两个分箱，共三组：12,23,34。然后分别计算三个绑定组的卡方值。
从计算的卡方值中找出最小的一个，并把这两个分箱合并：比如，23是卡方值最小的一个，那么就将2和3合并，本轮计算中分箱就变为了1,23,4。

背后的基本思想是：如果两个相邻的区间具有非常类似的类分布，那么这两个区间可以合并。否则，它们应该分开。低卡方值表明它们具有相似的类分布。（卡方值衡量推断值和观察值之间的偏离程度）
停止条件：1）卡方停止的阈值，2）分箱数目的限制

卡方分箱公式理解：
$\chi^{2}=\sum_{i=1}^{m} \sum_{j=1}^{k} \frac{\left(A_{i j}-E_{i j}\right)^{2}}{E_{i j}}$

m=2：表示相邻的两个分箱数目
k：表示目标变量的类别数，比如目标是网贷违约的好和坏，那么k=2。k也可以是多类，大于2。
$A_{ij}$ ：实际频数，即第i个分箱的j类频数
$E_{ij}$ ：期望频数

其中，期望频数的公式如下，可根据P(AB)=P(A)P(B)推导出来： $E_{i j}=\frac{R_{i} * C_{j}}{N}$ $R_{i}$ 、 $C_{j}$ ：分别是实际频数整列和整行的加和

举个例子说明一下这个公式是如何用的，对于相邻两个分箱的卡方值计算：
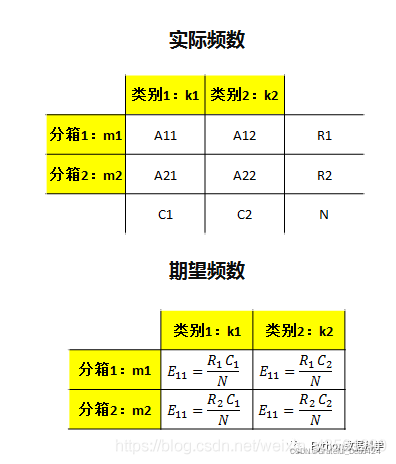
在这里插入图片描述
实际频数和期望频数都有了，带入卡方公式求解，过程如下： $\begin{aligned} \chi^{2} &=\sum_{i=1}^{m} \sum_{j=1}^{k} \frac{\left(A_{i j}-E_{i j}\right)^{2}}{E_{i j}} \\ &=\left[\frac{\left(A_{11}-E_{11}\right)^{2}}{E_{11}}+\frac{\left(A_{12}-E_{12}\right)^{2}}{E_{12}}\right]+\left[\frac{\left(A_{21}-E_{21}\right)^{2}}{E_{21}}+\frac{\left(A_{22}-E_{22}\right)^{2}}{E_{22}}\right] \end{aligned}$
如果计算结果是所有卡方值中最小的，说明：这组中两个分箱具有最相似的类分布，因此把它们合并。
在这里插入图片描述
如果性别和化妆与否没有关系，四个格子应该是括号里的数（期望值，用极大似然估计55=100*110/200，其中110/200可理解为化妆的概率，乘以男人数100，得到男人化妆概率的似然估计），这和实际值（括号外的数）有差距，理论和实际的差距说明这不是随机的组合。

应用拟合度公式
$\sum_{i=1}^{k} \frac{\left(f_{i}-n p_{i}\right)^{2}}{n p_{i}}=\frac{(95-55)^{2}}{55}+\frac{(15-55)^{2}}{55}+\frac{(85-45)^{2}}{45}+\frac{(5-45)^{2}}{45}=129.3$

决策树分箱

决策树分箱的原理就是用想要离散化的变量单变量用树模型拟合目标变量，例如直接使用sklearn提供的决策树（是用cart决策树实现的），然后将内部节点的阈值作为分箱的切点。
补充，cart决策树和ID3、C4.5决策树不同，cart决策树对于离散变量的处理其实和连续变量一样，都是将特征的所有取值从小到大排序，然后取两两之间的均值，然后遍历所有这些均值，然后取gini系数最小的点作为阈值进行划分数据集。并且该特征后续还可参与划分。
这里需要说明一下：cart的决策树是一颗二叉树，所以对于离散变量处理时会遍历所有值，然后取一个作为一类，剩下的作为另一类，这样建树的结果就是一颗二叉树；但在sklearn包并没有实现对离散属性的单独处理，所以我们传入的离散属性值也会被当成连续值去处理。“scikit-learn uses an optimised version of the CART algorithm; however, scikit-learn implementation does not support categorical variables for now.”

from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
x = np.array([0, 10, 180, 30, 55, 35, 25, 75, 80, 10]).reshape(-1, 1)
y = np.array([1, 1, 0, 1, 0, 0, 0, 1, 0, 0])boundary = []  # 待return的分箱边界值列表#x = x.fillna(-1).values  # 填充缺失值
#y = y.valuesclf = DecisionTreeClassifier(criterion='entropy',  # “信息熵”最小化准则划分max_leaf_nodes=6,  # 最大叶子节点数min_samples_leaf=0.05)  # 叶子节点样本数量最小占比clf.fit(x, y)  # 训练决策树
#DecisionTreeClassifier(criterion='entropy', max_leaf_nodes=6,
#                       min_samples_leaf=0.05)
plt.figure(figsize=(14,6))
tree.plot_tree(clf) #打印决策树的结构图
plt.show()

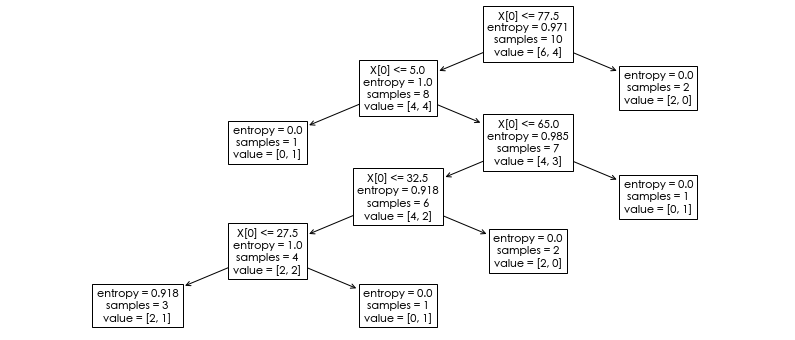
在这里插入图片描述

n_nodes = clf.tree_.node_count #决策树的节点数
n_nodes
#11
children_left = clf.tree_.children_left #node_count大小的数组，children_left[i]表示第i个节点的左子节点
children_right = clf.tree_.children_right #node_count大小的数组，children_right[i]表示第i个节点的右子节点
children_left
#array([ 1,  3, -1, -1,  5,  7, -1,  9, -1, -1, -1], dtype=int64)
children_right
#array([ 2,  4, -1, -1,  6,  8, -1, 10, -1, -1, -1], dtype=int64)
threshold = clf.tree_.threshold #node_count大小的数组，threshold[i]表示第i个节点划分数据集的阈值
threshold
#array([77.5,  5. , -2. , -2. , 65. , 32.5, -2. , 27.5, -2. , -2. , -2. ])
boundary1=[]
for i in range(n_nodes):if children_left[i] != children_right[i]:  # 非叶节点boundary1.append(threshold[i])boundary1.sort()
boundary1
#[5.0, 27.5, 32.5, 65.0, 77.5]
min_x = x.min()
max_x = x.max() + 0.1  # +0.1是为了考虑后续groupby操作时，能包含特征最大值的样本
boundary = [min_x] + boundary + [max_x]
boundary
#[0, 5.0, 27.5, 32.5, 65.0, 77.5, 180.1]