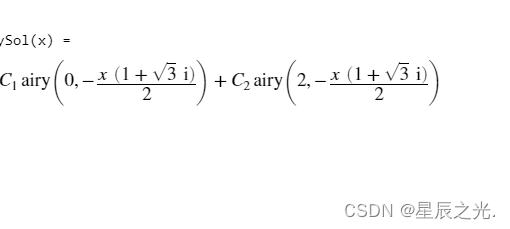显式欧拉

import numpy as np
from scipy.integrate import odeintdef f(x,y):return y-2*x/y
def f_ode(y,x):return y-2*x/ydef Explicit_Euler(f,a,b,y0,h):x_p = np.linspace(a,b,int(1/h)+1)n = len(x_p)value = np.zeros(n)value[0] = y0for i in range(1,n):value[i] = value[i-1]+h*f(x_p[i-1],value[i-1]) #x,y位置改了一下result=[i for j in odeint(f_ode,1,x_p) for i in j] #精确值，再转化为一维的for i in range(n):print('x={:.2f}时显式欧拉的误差为:{:.8f}'.format(x_p[i],abs(value[i]-result[i])))Explicit_Euler(f,0,1,1,0.2)

---

实验截图：

---

改进欧拉

import numpy as np
from scipy.integrate import odeintdef f(x,y):return y-2*x/y
def f_ode(y,x):return y-2*x/ydef Imporve_Euler(f,a,b,y0,h):x_p = np.linspace(a,b,int(1/h)+1)n = len(x_p)value = np.zeros(n)value[0] = y0for i in range(1,n):T1 = value[i-1]+h*f(x_p[i-1],value[i-1])T2 = value[i-1]+h*f(x_p[i],T1)value[i] = (T1+T2)/2result=[i for j in odeint(f_ode,1,x_p) for i in j] #精确值，再转化为一维的for i in range(n):print('x={:.2f}时显式欧拉的误差为:{:.8f}'.format(x_p[i],abs(value[i]-result[i])))Imporve_Euler(f,0,1,1,0.2)

---

实验截图：

---

龙格库塔

import numpy as np
from scipy.integrate import odeintdef f(x,y):return y-2*x/y
def f_ode(y,x):return y-2*x/ydef Runge_kutta(f,a,b,y0,h):x_p = np.linspace(a,b,int(1/h)+1)n = len(x_p)value = np.zeros(n)value[0] = y0for i in range(1,n):k1 = f(x_p[i-1],value[i-1])k2 = f(x_p[i-1]+h/2,value[i-1]+h/2*k1)k3 = f(x_p[i-1]+h/2,value[i-1]+h/2*k2)k4 = f(x_p[i-1]+h,value[i-1]+h*k3)value[i] = value[i-1]+h/6*(k1+2*k2+2*k3+k4)result=[i for j in odeint(f_ode,1,x_p) for i in j] #精确值，再转化为一维的for i in range(n):print('x={:.2f}时显式欧拉的误差为:{:.8f}'.format(x_p[i],abs(value[i]-result[i])))Runge_kutta(f,0,1,1,0.2)

---

实验截图：

方法	显式欧拉误差	改进欧拉误差	龙格库塔误差
x=0.2	0.01678407	0.00345073	0.00001336
x=0.4	0.03169259	0.00667151	0.00002618
x=0.6	0.04825549	0.01046424	0.00004181
x=0.8	0.06863307	0.01540958	0.00006254
x=1.0	0.09489743	0.02215388	0.00009113