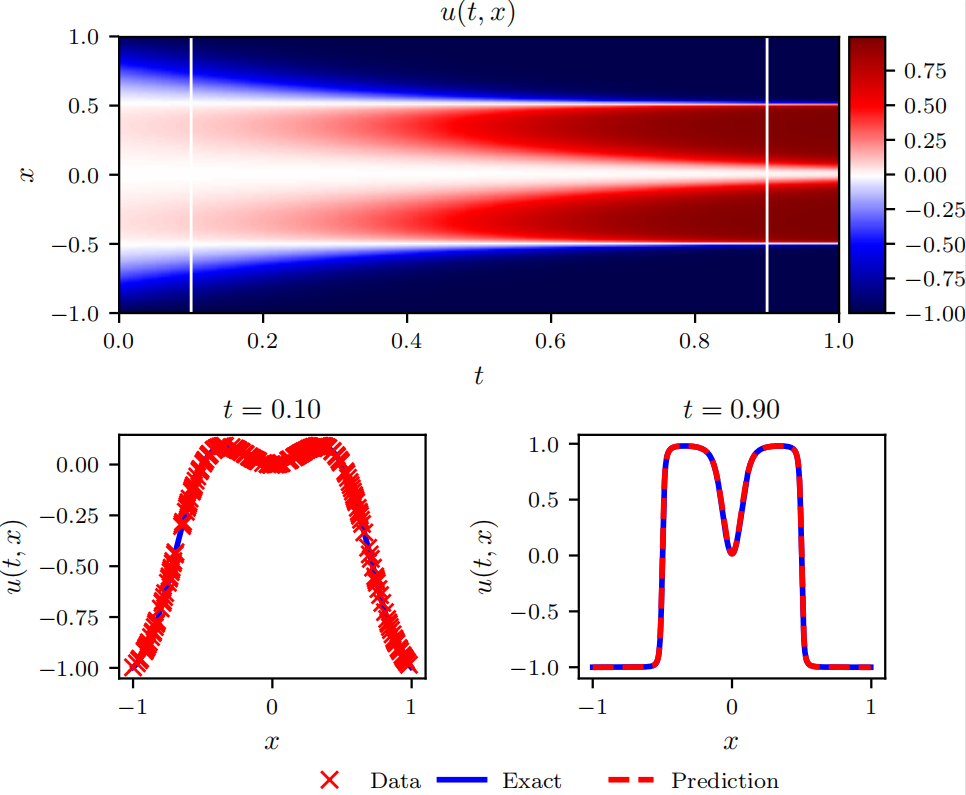
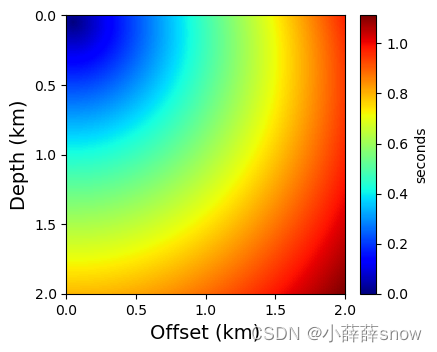
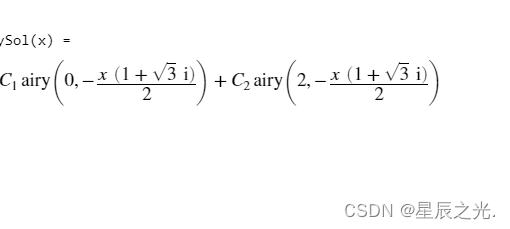本文介绍两种入门级求解微分方程的方法 —— 梯形法与欧拉法。

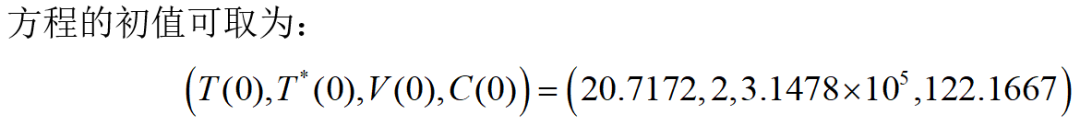
将上述方程组改写成matlab语言:
function F = fun(t,Y)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %
% 程序作者:Miracle (matlab爱好者公众号) %
% %
% 欢迎关注matlab爱好者公众号 %
% %
% 任何人都可以免费无条件获取本程序,切勿将本程序用于商业用途。%
% 程序版权归matlab爱好者公众号所有。%
% %
% 敬告:切勿删改本声明部分,否则将自动失去本程序的使用权 %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 把初值传给T、T、V、C
T = Y(1);
Tx = Y(2);
V = Y(3);
C = Y(4);
% 设置对应的微分方程
f1 = 1 - 0.1*T + 0.5*T*(1 - (T + Tx)/1000) - 0.0014*V*T;
f2 = 0.0014*V*T - 0.9*Tx - 0.03*Tx*C;
f3 = 3.09375*Tx - (3+0.007*T)*V;
f4 = 0.03*Tx*C-0.06*C;
% 放在一起
F = [f1;f2;f3;f4];
end一、欧拉法
1.1 向前欧拉公式

1.2 向后欧拉公式

欧拉法求解源代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %
% 程序作者:Miracle (matlab爱好者公众号) %
% %
% 欢迎关注matlab爱好者公众号 %
% %
% 任何人都可以免费无条件获取本程序,切勿将本程序用于商业用途。%
% 程序版权归matlab爱好者公众号所有。%
% %
% 敬告:切勿删改本声明部分,否则将自动失去本程序的使用权 %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear;clc;close all;
Delta = 0.001; %定义步长
t = 0:Delta:50; %定义自变量t
n = length(t); %自变量长度n
Y(:,1) = [20.7172;2;3.1478*10^5;122.1667]; %定义T T* V C的初始值%% 自定义欧拉法,求解微分方程组
for k = 1:n-1%向前欧拉法%Y(:,k+1) = Y(:,k) + Delta*f(t(k),Y(:,k));Y(:,k+1) = Y(:,k) + Delta*f(t(k),Y(:,k));Y(:,k+1) = Y(:,k) + Delta*f(t(k+1),Y(:,k+1));
end
% 给T、T*、V、C赋值
T = Y(1,:);
T_xing = Y(2,:);
V = Y(3,:);
C = Y(4,:);
%% 绘制图像
figure;
set(gcf,'units','normalized','position',[0.15 0.2 0.7 0.6]);
subplot(2,2,1);
plot(t,T,'linewidth',1);xlabel('t');ylabel('T');title('T');
subplot(2,2,2);
plot(t,T_xing,'linewidth',1);xlabel('t');ylabel('T^*');title('T^*');
subplot(2,2,3);
plot(t,V,'linewidth',1);xlabel('t');ylabel('V');title('V');
subplot(2,2,4)
plot(t,C,'linewidth',1);xlabel('t');ylabel('C');title('C');欧拉法结果图
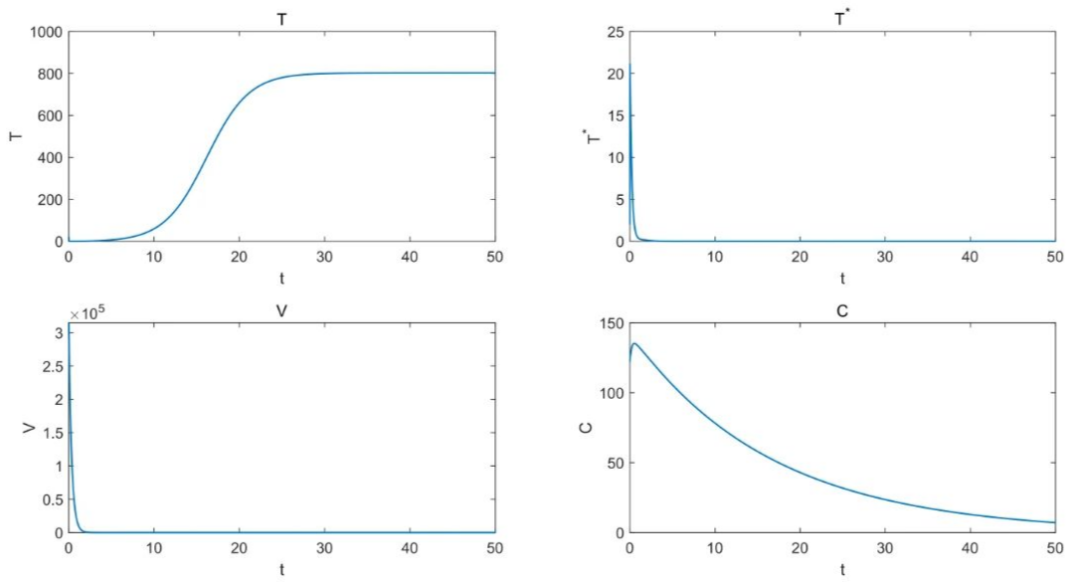
二、梯形法
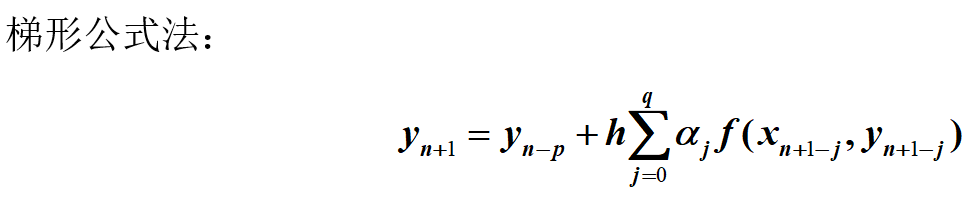
梯形法求解源代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %
% 程序作者:Miracle (matlab爱好者公众号) %
% %
% 欢迎关注matlab爱好者公众号 %
% %
% 任何人都可以免费无条件获取本程序,切勿将本程序用于商业用途。%
% 程序版权归matlab爱好者公众号所有。%
% %
% 敬告:切勿删改本声明部分,否则将自动失去本程序的使用权 %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear;clc;close all;
Delta = 0.001; % 定义步长
t = 0:Delta:50; % 定义自变量t
n = length(t); % 自变量长度n
Y(:,1) = [20.7172;2;3.1478*10^5;122.1667];%定义T T* V C的初始值%% 自定义梯形公式法,求解微分方程组
for k = 1:n-1 Y(:,k+1) = Y(:,k) + Delta*f(t(k),Y(:,k));Y(:,k+1) = Y(:,k) + Delta*(f(t(k),Y(:,k))+f(t(k+1),Y(:,k+1)));
end
% 给T、T*、V、C赋值
T = Y(1,:);
T_xing = Y(2,:);
V = Y(3,:);
C = Y(4,:);
%% 绘制图像
figure;
set(gcf,'units','normalized','position',[0.15 0.2 0.7 0.6]);
subplot(2,2,1);plot(t,T,'linewidth',1);xlabel('t');ylabel('T');title('T');
subplot(2,2,2);plot(t,T_xing,'linewidth',1);xlabel('t');ylabel('T^*');title('T^*');
subplot(2,2,3);plot(t,V,'linewidth',1);xlabel('t');ylabel('V');title('V');
subplot(2,2,4);plot(t,C,'linewidth',1);xlabel('t');ylabel('C');title('C');梯形法结果图
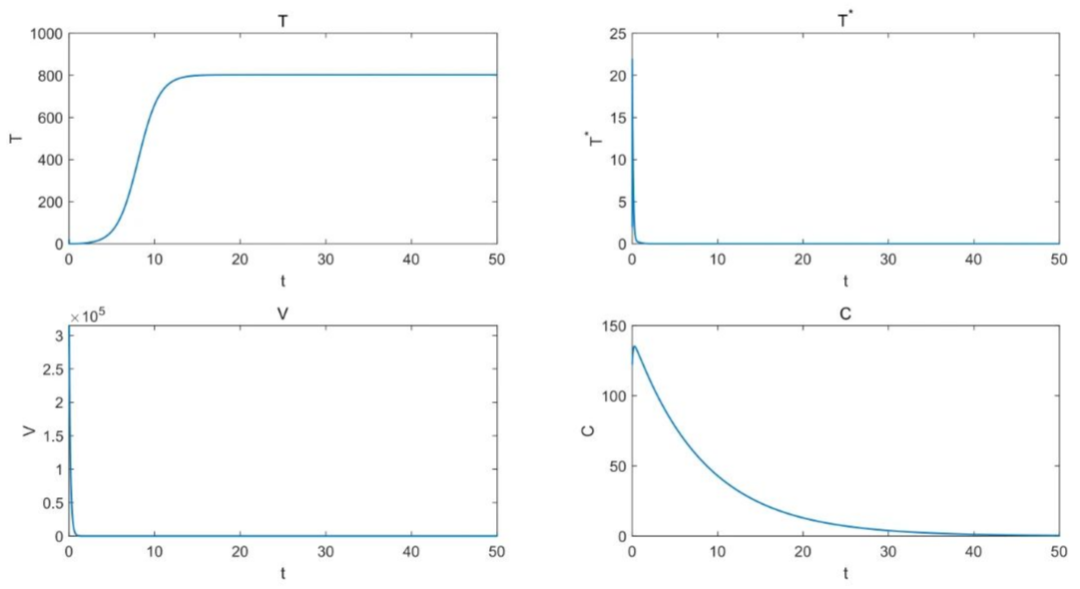
感谢Miracle向公众号投稿!欢迎更多爱好、喜欢matlab编程的朋友来稿,在公众号回复“投稿”了解投稿详情。
参考资料:
[1] https://blog.csdn.net/weixin_42141390/article/details/110184743
[2] https://blog.csdn.net/misskissC/article/details/8913941
图片来源:由 Gerd Altmann 在Pixabay上发布