原理解读

prophet与常用的自回归时间序列预测模型一样，本质上都是拟合过去，预测未来。作者雨中不同的视角是：在某些特殊日期，可能受到活动、节假日等影响，时间序列会产生一定的波动，因此作者将节假日序列引入了时间序列分解；同时作者在分解/拟合 趋势项的时候考虑到了趋势随时间的自然变化，引入了变点（change point）的概念，更有利于趋势项的拟合。

一、时间序列的分解

常见的自回归时间序列预测模型都需要进行时间序列分解，这是一种常见的时间序列预处理方式，将一个时间序列分解为多个时间序列目的是为了挖掘出序列自身的一些规律。
时间序列分解主要分为加法形式和乘法形式。

加法形式：

乘法形式：

而乘法形式等价于加法形式：

注：季节项 St ，趋势项Tt，剩余项 Rt
因此facebook的工程师定义了如下时间序列分解：

注：g(t)趋势项，s(t)周期项，h(t)节假日项，Et表示误差项或者称为剩余项，服从正态分布。

二、趋势项模型

基于逻辑回归的趋势项

注：C称为曲线的最大渐近值， k表示曲线的增长率， m表示曲线的offset parameter（我理解为，类似于线性回归y=kx+b中的b）
在 Prophet 里面，作者考虑最大渐近值、曲线的增长率、offset parameter都不会随着时间变化一成不变，理应是一个随时间变化的参数，因此将上述三个参数全部换成了随着时间而变化的函数：

定义变点（change point）

变点：曲线的趋势不会一直不变，在某些特定的时候或者有着某种潜在的周期曲线会发生变化。如图所示，很好理解

假设S个变点：

一旦变化量k确定了，另外一个参数 m也随之确定。在这里需要把线段的边界处理好，因此通过数学计算可以得到（论文没有给出推导公式）：

逻辑回归的趋势项最终公式：

基于线性回归的趋势项

本质上其实是分段线性函数，适用于不表现出饱和增长的预测问题。

在分段线性函数中变化率的计算通逻辑斯特回归，同时为了使函数连续：

变点的选择

趋势的变化主要与三个参数有关：1、changepoint_range，2、n_changepoint，3、changepoint_prior_scale

changepoint_range 指的是百分比，需要在前 changepoint_range 那么长的时间序列中设置变点，在默认的函数中是 changepoint_range = 0.8。
n_changepoint 表示变点的个数，在默认的函数中是 n_changepoint = 25，表示前changepoint_range范围内均匀分布25个变点。
changepoint_prior_scale 表示变点增长率的分布情况，这里的 τ 就是 change_point_scale。

为什么要用laplace分布来拟合change_point_scale？ 我个人的理解：laplace分布更多的点靠近x=0，即表示再多多数情况下即使这个点设置为了变点，但是在拟合时依然将其变化率的变化设置为零，防止过拟合。
对未来的预估：

三、季节性趋势

在数学分析中，区间内的周期性函数是可以通过正弦和余弦的函数来表示的。假设 f(x)是以2*pi为周期的函数，那么它的傅立叶级数就是：

假设 P 表示时间序列的周期，它的傅立叶级数的形式是：

作者经验：P=365,N=10;P=7,N=3.
当N=3:


这一点很好理解，方差越大，表示可以拟合的有离散点变化可以较复杂（变化多样），因此该级数函数可以拟合更复杂的离散点，因此值越大，可以拟合更复杂的季节效应（值太大，也有可能导致过拟合）。

四、节假日影响

对与第 i个节假日来说，Di表示该节假日的前后一段时间，即节假日的影响范围。

表示节假日的影响程度，v=holidays_prior_scale 默认值是 10，当值越大时，表示节假日对模型的影响越大（原理同上）。

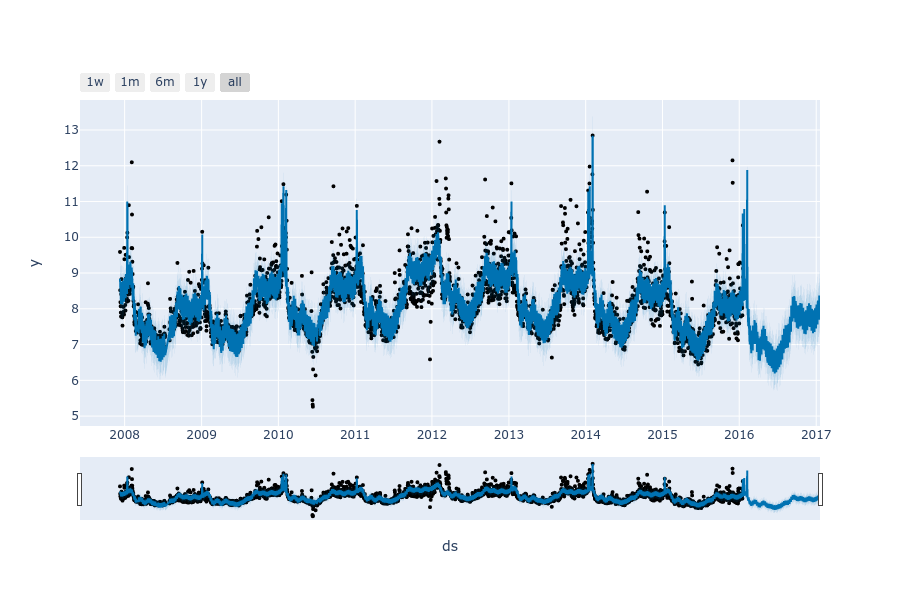
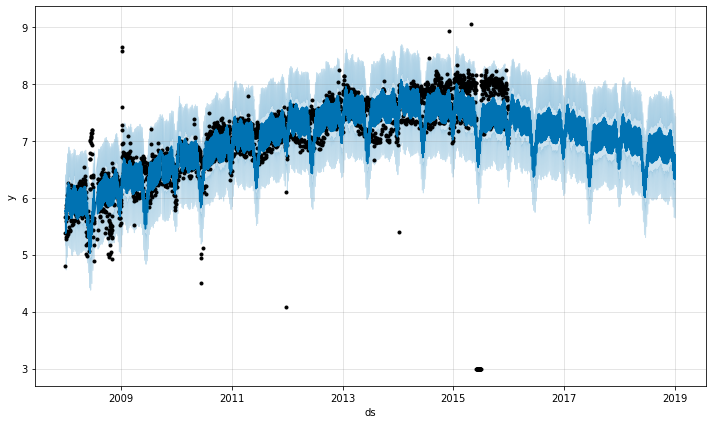
模型实战

后续补充