论文标题：Frequency-Hiding Order-Preserving Encryption

原文作者：Florian Kerschbaum， Authors Info & Claims

原文链接：https://dl.acm.org/doi/abs/10.1145/2810103.2813629

发表会议：CCS '15: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security

· 简介

· 术语介绍

· 基于问题

· 安全性定义

· 方案构造

· 安全性证明

· 简介

保序加密技术可以被用于对加密的数据进行有效的范围查询，这也使得保序加密更加适合用于数据外包的云计算场景，但目前的保序加密技术的安全性仍然存在着一些争议。本文主要是提出了一种保序加密方案，通过随机化密文来隐藏明文的频率，比以往的方案安全性更高并且存储规模仍然很小。该方案中的密文近似均匀分布，从而提高了对频率分析攻击的抵抗能力。因此可以更安全地外包大型数据库，其安全性也会随着数据集的增大而增加。

· 术语介绍

1. 保序加密 (order-preserving encryption）

密文保持了明文顺序特征的一种加密方案，即如果明文 $a$ 和 $b$ 满足 $a<b$ ，那么经过加密后的密文 $E(a)$ 和 $E(b)$ 也满足 $E(a)<E(b)$ 。

2. 有状态的保序加密方案 (stateful order-preserving encryption)

一个有状态的保序加密方案 $\Pi _{FHOPE}$ 通常由以下三个算法组成：

$S\leftarrow KeyGen(\lambda)$ ：通过一个安全参数 $\lambda$ 生成一个密钥状态 $S$ ;
$y \leftarrow Encrypt(S, x)$ ：计算明文 $x$ 对应的密文 $y$ ,并将状态更新到 $S'$ ;
$x\leftarrow Decrypt(S, y)$ ：基于状态 $S$ 和密文 $y$ ，解密出明文 $x$ 。

有状态的保序加密方案和无状态的保序加密方案的区别：

有状态的保序加密方案需要在加密和解密操作之间保持某种状态，以便进行正确的解密操作。这个状态可能是一个密钥，或者是一个随机数或计数器等。在加密操作时，这个状态被用来生成密文；在解密操作时，这个状态被用来还原明文。由于状态的存在，这种方案可能需要更多的存储空间，并且可能需要更多的计算来管理状态。相比之下，无状态的保序加密方案不需要在加密和解密操作之间保持任何状态。它们使用一些固定的参数来生成密文，并使用相同的参数来解密密文。由于无需维护状态，这种方案通常需要更少的存储空间，并且可以更快速地进行加密和解密操作。需要注意的是，虽然无状态的保序加密方案具有一些优势，但它们可能更容易受到一些攻击，例如频谱分析和差分攻击。因此，在选择加密方案时，需要考虑到具体的应用场景和安全需求。

3. IND-OCPA security

ND代表不可区分性（indistinguishability），OCPA代表选择明文攻击（chosen plaintext attack）下的安全性。

在IND-OCPA安全模型下，攻击者可以选择一些明文并获得相应的密文，然后尝试通过分析这些密文来破解密钥。在这个过程中，攻击者不能直接访问密钥，但可以进行大量的"明文-密文"查询。如果方案在这种攻击下是安全的，那么攻击者无法获得有用的信息，IND-OCPA安全是公钥加密方案中最基本的安全性要求之一，也是目前保序加密方案最强的安全性，也就是除了顺序以外不泄露任何有关明文的信息。

IND-OCPA安全被定义为challenger和adversary之间的一个game：adversary准备两个明文序列，其中两个序列具有相同的顺序，并且序列中的每个明文是不同的。他把这两个序列发送给challenger。challenger对其中一个序列进行加密，并将密文发送给adversary，adversary猜测它是两个序列中的哪一个。

· 基于问题

在外包的数据库（结构化数据）中，数据库表的每一列都被进行加密，例如，在一个关于用户的典型数据库表中，会有诸如名字和姓氏、出生日期、性别等字段，每个字段都用各自对应的密钥进行加密。然而，在大多数这些字段中，输入并不是均匀分布的。史密斯的姓氏在美国肯定比赫克斯特布尔更常见。事实上，研究表明，即使是部分频率信息，就像可搜索加密的情况一样，也可以有很的高概率被解密条目。对于一个典型的数据库中的许多字段，关于频率分布的信息是很容易获得的，例如，许多网站列出了每个地区最常见的名字和姓氏。于是本文提出了一种保序加密方案，重复的明文可以映射为不同的密文但仍然保持其顺序信息。

· 安全性定义

将上述介绍过的IND-OCPA安全扩展到随机化密文的保序加密方案中。那么 IND-FAOCPA安全定义的目标是：密文只泄露明文的随机顺序，即两个具有相同随机顺序的序列（但不同的明文频率）应该是无法区分的。本文定义了以下的 security game $Game_{FAOCPA} (\lambda )$ ：

有了以上game，我们现在可以定义针对频率分析有序选择明文攻击的安全性：

如果敌手A在 $Game_{FAOCPA} (\lambda )$ 中输出 $c$ 的概率可以忽略不计，即：

$Pr[A(Game_{FAOCPA} (\lambda ))=c]<\frac{1}{2} +\frac{1}{Poly(\lambda )}$ ,那么一个有状态的保序加密方案 $\Pi _{FHOPE}$ 在频率分析顺序选择明文攻击下是满足 IND-FAOCPA安全的。

· 方案构造

同mOPE一样，本文数据的存储方式也是以二叉树的数据结构，但是增加了两个参数，如下图所示：

参数介绍： $n$ 为要插入的所有的明文的数量， $N$ 为不同明文的个数。因此，上述算法1中的位长度为 $k=\left \lceil log_{2} N \right \rceil$ 。 $\lambda$ 为密文的安全参数，因此，在算法1中的 $l=\lambda k$ ,安全参数也可以用于确定伪随机性的种子的长度。

接下来，现在我们执行下述算法2中的加密。我们将二叉搜索树(状态)表示为节点 $\left \{ t \right \}$ 的集合 $T$ ，此外，为当前节点添加输入 $t$ ，为下限和上限添加最小值和最大值，以实现递归。(注：最大值和最小值表示了当前的明文加密以后可能的密文的上限和下限）

其中，第5步中的 $REBALANCE()$ 算法表示重新平衡这棵二叉树（这里我的理解是：如果新插入的这个明文和 $max$ 之差小于2的话，这个明文对应的密文就别无选择了，也很容易被频率攻击猜到这个明文是可能和上一个结点中存储的明文相等的）：

了解了以上过程后，我们可以举个例子：假如我们有一个明文序列 $X=1,2,1,3$ ,具有 $min=-1$ 和 $max=128$ 。然后前两个明文 $1,2$ 对应的密文是确定的 $y_{1} =64$ 和 $y_{2} =96$ 。那么对于第三个明文 $x_{3} =1$ ，由于它和 $x_{1} =1$ 是两个重复的明文，所以这里要对它进行随机化以隐藏明文的频率。那么现在树的结构有如下两种情况：

情况1：

此时，加密算法执行到第1步，此时 $t.plain=2$ ,跳转到第7步，由于 $t$ 的左子树不为空，所以递归到 $t.plain=1$ ，此时若随机取的 $coin=0$ ,且此时 $t$ 的左子树为空，所以明文 $x_{3} =1$ 加密后的密文应该是 $min+\left \lceil \frac{t.cipher-min}{2} \right \rceil =-1+\left \lceil \frac{64-(-1)}{2} \right \rceil =-1+33=32$ ;若随机取的

$coin=1$ ,并且此时 $t$ 的右子树为空，加密后的密文应该是 $t.cipher+\left \lceil \frac{max-t.cipher}{2} \right \rceil =64+\left \lceil \frac{128-(64)}{2} \right \rceil =64+64=112$ $y_{3} =48$

情况2：

同理，加密算法执行到第1步，此时 $t.plain=1$ ,如果随机取的 $coin=0$ ，此时 $t$ 的左子树为空，所以明文 $x_{3} =1$ 加密后的密文应该是 $min+\left \lceil \frac{t.cipher-min}{2} \right \rceil =-1+\left \lceil \frac{64-(-1)}{2} \right \rceil =-1+33=32$ ;若随机取的

$coin=1$ ,并且此时 $t$ 的右子不树为空，所以递归到 $t.plain=2$ ，加密后的密文应该是 $min+\left \lceil \frac{t.cipher-min}{2} \right \rceil =-1+\left \lceil \frac{96-(-1)}{2} \right \rceil =-1+49=48$ 。

综上所述，明文 $x_{3} =1$ 随机化后的密文值可能是 $y_{1} =32$ , $y_{1} =32$ ,和 $y_{3} =48$ 。

那么再假设我们有一个明文序列 $X=0,1,0,1$ ，那么最终的树可能如下图所示：

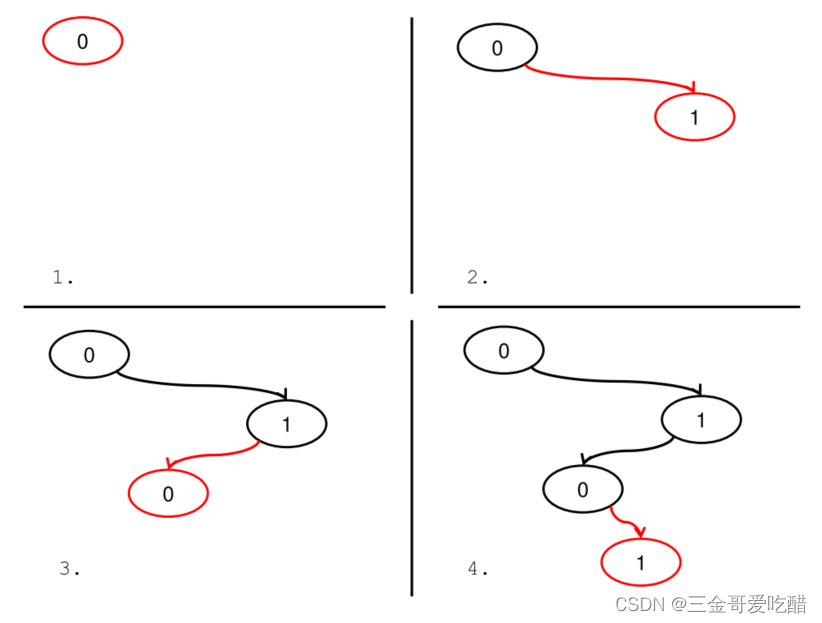
每一次插入新的节点的时候，不难看出，重复的明文可以作为具有相同明文结点的子节点，也可以作为具有不同明文结点的子节点，这取决与我们算法2中 $coin$ 的随机取值情况。

由于相比于正式的算法 $\Pi _{FHOPE}$ ，我们在算法2中添加了递归输入 $t$ ，所以相应的解密算法调用 $Decrypt (x)$ 最终会递归到 $Decrypt(x, root(T ))$ ：

· 安全性证明

通过构造一个加密模拟器，为两个挑战序列中的每一个产生相同的输出来证明。因此，计算的不可区分性源于将随机源实现为伪随机函数而不是任何其他硬度假设。模拟器的算法如下：

而对于算法5中的coin的随机取法，这里也定义了一个随机算法：

算法7的输出是确定性的，而 $\gamma _{i}$ 和 $\gamma _{v}$ 的选择则由算法6决定。算法6在所有可能的随机顺序中均匀地选择一个随机顺序。由于每个随机顺序的结果是不同的二叉搜索树，而随机coin函数的每个输出也产生不同的二叉搜索树，因此算法7的输出与统一的随机coin算法是难以区分的。所以在算法中敌手赢得 $Game_{FAOCPA} (\lambda )$ 的概率减去 $\frac{1}{2}$ 是可忽略级别的。