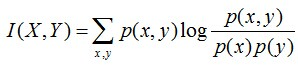信息论（熵的基础）

熵

相对熵（KL散度）

交叉熵

机器学习中交叉熵的应用

为什么要用交叉熵做loss函数？

交叉熵在单分类问题中的使用

交叉熵在多分类问题中的使用

sigmoid激活函数（承接上面多分类用Sigmoid不用Softmax）

代码实现

画图

softmax激活函数

Softmax主要优点

实现代码

多类分类及多标签分类（承接上面Sigmoid在多标签中的应用）

多类分类定义

多标签定义

使用softmax和sigmoid激活函数来做多类分类和多标签分类

softmax激活函数应用于多类分类

sigmoid激活函数应用于多标签分类

binary_cross_entropy二分类交叉熵（承接上面多标签使用binary_cross_entropy损失函数）

softmax_cross_entropy

softmax_cross_entropy_with_logits计算过程

sigmoid_cross_entropy

交叉熵（cross entropy）是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。

https://blog.csdn.net/tsyccnh/article/details/79163834

信息论（熵的基础）

交叉熵是信息论中的一个概念。

信息论的基本想法是一个不太可能的事件居然发生了，要比一个非常可能的事件发生，能提供更多的信息。

要想了解交叉熵的本质，需要先从最基本的概念讲起。

首先是信息量。假设我们听到了两件事，分别如下：
事件A：巴西队进入了2018世界杯决赛圈。
事件B：中国队进入了2018世界杯决赛圈。
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

再举一例：（https://www.cnblogs.com/huangtao36/p/7763405.html）

“今天早上太阳升起”，这是一件很平常的事情，信息量是如此之少以至于没有必要发送，但一条消息说：“今天早上有日食”，这件事发生概率很小，信息量就很丰富。

在机器学习中，主要使用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。

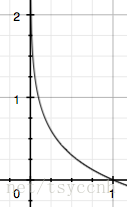
假设x是一个离散型随机变量，其取值集合为X,概率分布函数p(x)=Pr(X=x),x∈Xp(x)=Pr(X=x),x∈X,则定义事件 $X=x_0$ 的信息量为：

$I(x_0)=-log(p(x_0))$

由于是概率所以p(x0)的取值范围是[0,1],绘制为图形如下：

该函数符合我们对信息量的直觉

熵

考虑另一个问题，对于某个事件，有n种可能性，每一种可能性都有一个概率 $p(x_i)$
这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量

我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：

$H(X)=-\sum_{i=1}^n p(x_i)log(p(x_i))$

其中n代表所有的n种可能性，所以上面的问题结果就是

$\begin{eqnarray} H(X)&=&-[p(A)log(p(A))+p(B)log(p(B))+p(C))log(p(C))]\\ &=&0.7\times 0.36+0.2\times 1.61+0.1\times 2.30\\ &=&0.804 \end{eqnarray}$

然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式：

$\begin{eqnarray} H(X)&=&-\sum_{i=1}^n p(x_i)log(p(x_i))\\ &=&-p(x)log(p(x))-(1-p(x))log(1-p(x)) \end{eqnarray}$

相对熵（KL散度）

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异

维基百科对相对熵的定义

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]。直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式：

$D_{KL}(p||q)=\sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)})$

n为事件的所有可能性。
$D_{KL}$ 的值越小，表示q分布和p分布越接近

交叉熵

对上面公式 $D_{KL}(p||q)=\sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)})$ 变形可以得到：

$\begin{eqnarray} D_{KL}(p||q) &=& \sum_{i=1}^np(x_i)log(p(x_i))-\sum_{i=1}^np(x_i)log(q(x_i))\\ &=& -H(p(x))+[-\sum_{i=1}^np(x_i)log(q(x_i))] \end{eqnarray}$

等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：

$H(p,q)=-\sum_{i=1}^np(x_i)log(q(x_i))$

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即 $D_{KL}(y||\hat{y})$ ，由于KL散度中的前一部分−H(y)−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

机器学习中交叉熵的应用

为什么要用交叉熵做loss函数？

在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如：

$loss = \frac{1}{2m}\sum_{i=1}^m(y_i-\hat{y_i})^2$

这里的m表示m个样本的，loss为m个样本的loss均值。
MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

交叉熵在单分类问题中的使用

这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。
交叉熵在单分类问题上基本是标配的方法：

$loss=-\sum_{i=1}^{n}y_ilog(\hat{y_i}) \tag{2.1}$

上式为一张样本的loss计算方法。上式n代表着n种类别。
举例说明,比如有如下样本：

对应的标签和预测值

那么：

$\begin{eqnarray} loss&=&-(0\times log(0.3)+1\times log(0.6)+0\times log(0.1) &=&-log(0.6) \end{eqnarray}$

对应一个batch的loss就是：

$loss=-\frac{1}{m}\sum_{j=1}^m\sum_{i=1}^{n}y_{ji}log(\hat{y_{ji}})$

m为当前batch的样本数，n代表着n种类别。

交叉熵在多分类问题中的使用

这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗
和单分类问题的标签不同，多分类的标签是n-hot。
比如下面这张样本图，即有青蛙，又有老鼠，所以是一个多分类问题。

对应的标签和预测值：

值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid (两者区别见下文)。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。前面说过对于二项分布这种特殊的分布，熵的计算可以进行简化。

同样的，交叉熵的计算也可以简化，即：

$loss =-ylog(\hat{y})-(1-y)log(1-\hat{y})$

注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。
例子中可以计算为：

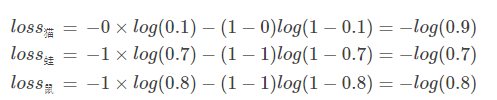
sigmoid激活函数（承接上面多分类用Sigmoid不用Softmax）

https://blog.csdn.net/uncle_ll/article/details/82778750

Sigmoid激活函数的计算公式如下：

$S(x)={\frac {1}{1+e^{-x}}}.$

x: 输入
float：表示浮点型数据
exp：对其求指数
f(x): 函数输出

代码实现

# Required Python Package
import numpy as npdef sigmoid(inputs):"""Calculate the sigmoid for the give inputs (array):param inputs::return:"""sigmoid_scores = [1 / float(1 + np.exp(- x)) for x in inputs]return sigmoid_scoressigmoid_inputs = [2, 3, 5, 6]
print "Sigmoid Function Output :: {}".format(sigmoid(sigmoid_inputs))

经过sigmoid函数计算后获得Sigmoid分数。函数输出：

Sigmoid Function Output :: [0.8807970779778823, 0.9525741268224334, 0.9933071490757153, 0.9975273768433653]

画图

# Required Python Packages
import numpy as np
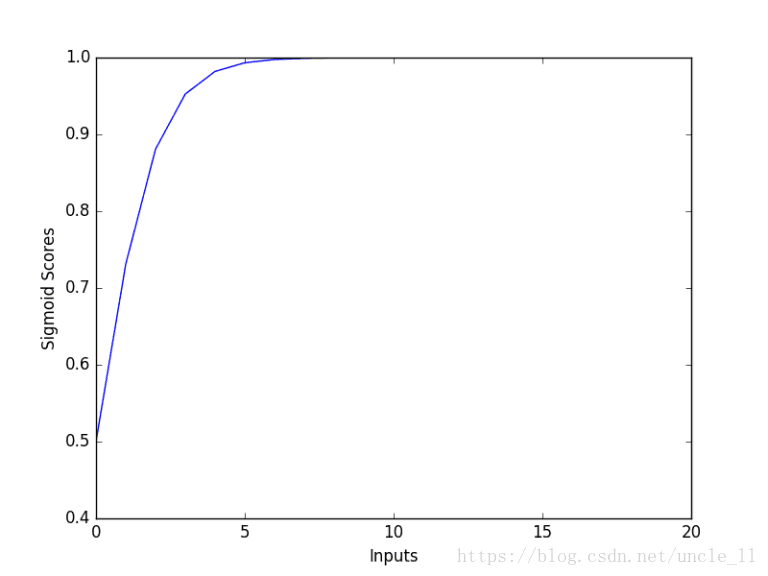
import matplotlib.pyplot as pltdef sigmoid(inputs):"""Calculate the sigmoid for the give inputs (array):param inputs::return:"""sigmoid_scores = [1 / float(1 + np.exp(- x)) for x in inputs]return sigmoid_scoresdef line_graph(x, y, x_title, y_title):"""Draw line graph with x and y values:param x::param y::param x_title::param y_title::return:"""plt.plot(x, y)plt.xlabel(x_title)plt.ylabel(y_title)plt.show()graph_x = range(0, 21)
graph_y = sigmoid(graph_x)print "Graph X readings: {}".format(graph_x)
print "Graph Y readings: {}".format(graph_y)line_graph(graph_x, graph_y, "Inputs", "Sigmoid Scores")

脚本输出：

Graph X readings: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]Graph Y readings: [0.5, 0.7310585786300049, 0.8807970779778823, 0.9525741268224334, 0.9820137900379085, 0.9933071490757153, 0.9975273768433653, 0.9990889488055994, 0.9996646498695336, 0.9998766054240137, 0.9999546021312976, 0.999983298578152, 0.9999938558253978, 0.999997739675702, 0.9999991684719722, 0.999999694097773, 0.9999998874648379, 0.9999999586006244, 0.9999999847700205, 0.9999999943972036, 0.9999999979388463]

从上图可以看出，随着输入值的增加，sigmoid得分增加到1。

softmax激活函数

Softmax主要优点

输出概率的范围为0到1，所有概率的和将等于1。如果将softmax函数用于多分类模型，它会返回每个类别的概率，并且目标类别的概率值会很大。

softmax激活函数的计算公式如下：

$\sigma (\mathbf {z} )_{j}={\frac {e^{z_{j}}}{\sum _{k=1}^{K}e^{z_{k}}}}$

x: 输入
exp：对其求指数
f(x): 函数输出

从上述计算公式可以看出：

计算出的概率将在0到1的范围内。
所有概率的和等于1。

实现代码

# Required Python Package
import numpy as npdef softmax(inputs):"""Calculate the softmax for the give inputs (array):param inputs::return:"""return np.exp(inputs) / float(sum(np.exp(inputs)))softmax_inputs = [2, 3, 5, 6]
print "Softmax Function Output :: {}".format(softmax(softmax_inputs))

脚本输出：

Softmax Function Output :: [ 0.01275478  0.03467109  0.25618664  0.69638749]

画图：

# Required Python Packages
import numpy as np
import matplotlib.pyplot as pltdef softmax(inputs):"""Calculate the softmax for the give inputs (array):param inputs::return:"""return np.exp(inputs) / float(sum(np.exp(inputs)))def line_graph(x, y, x_title, y_title):"""Draw line graph with x and y values:param x::param y::param x_title::param y_title::return:"""plt.plot(x, y)plt.xlabel(x_title)plt.ylabel(y_title)plt.show()graph_x = range(0, 21)
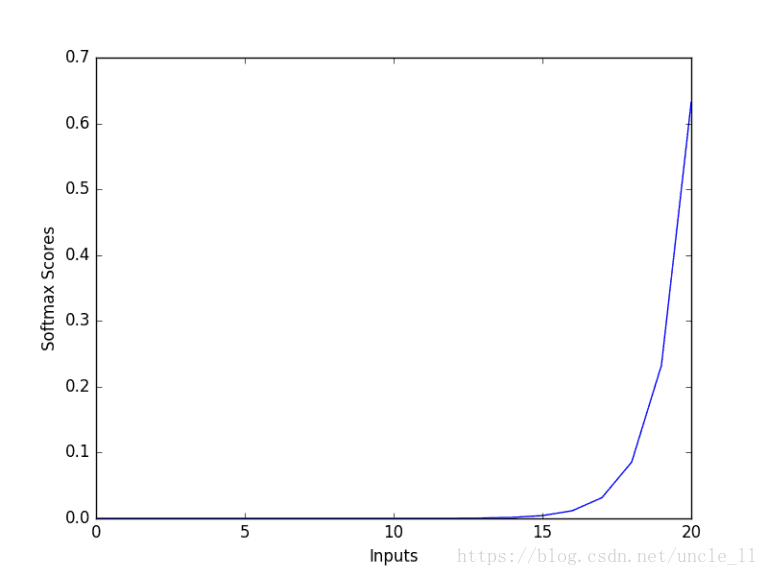
graph_y = softmax(graph_x)print "Graph X readings: {}".format(graph_x)
print "Graph Y readings: {}".format(graph_y)line_graph(graph_x, graph_y, "Inputs", "Softmax Scores")

脚本输出：

Graph X readings: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
Graph Y readings: [ 1.30289758e-09 3.54164282e-09 9.62718331e-09 2.61693975e-08 7.11357976e-08 1.93367146e-07 5.25626399e-07 1.42880069e-06 3.88388295e-06 1.05574884e-05 2.86982290e-05 7.80098744e-05 2.12052824e-04 5.76419338e-04 1.56687021e-03 4.25919483e-03 1.15776919e-02 3.14714295e-02 8.55482149e-02 2.32544158e-01 6.32120559e-01]

该图显示了softmax函数的基本属性，输入值越大，其概率越高。

多类分类及多标签分类（承接上面Sigmoid在多标签中的应用）

多类分类定义

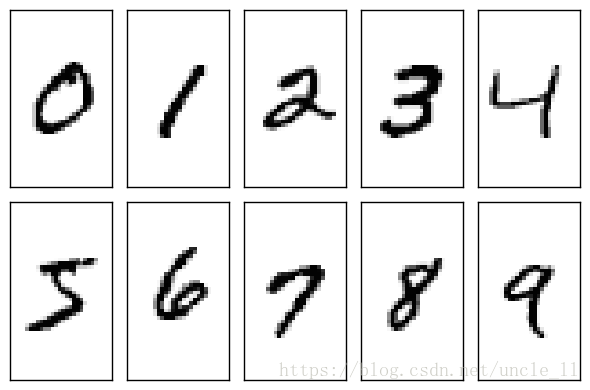
意味着候选集是一个多分类，而不仅仅是二分类，不是是与否的问题，而是属于多类中哪一类的问题。一个样本属于且只属于多个分类中的一个，一个样本只能属于一个类，不同类之间是互斥的。举例而言，MNIST数据集，常用的数字手写体识别数据集，它的标签是一个多分类的过程，要将数字手写体识别为0~9中的某一个数字：

多标签定义

一个样本的标签不仅仅局限于一个类别，可以具有多个类别，不同类之间是有关联的。比如一件衣服，其具有的特征类别有长袖、蕾丝等属性等，这两个属性标签不是互斥的，而是有关联的。

使用softmax和sigmoid激活函数来做多类分类和多标签分类

在实际应用中，一般将softmax用于多类分类的使用之中，而将sigmoid用于多标签分类之中。

softmax激活函数应用于多类分类

假设神经网络模型的最后一层的全连接层输出的是一维向量logits=[1,2,3,4,5,6,7,8,9,10],这里假设总共类别数量为10，使用softmax分类器完成多类分类问题，并将损失函数设置为categorical_cross_entropy损失函数：
用tensorflow实现：

tf.argmax(tf.softmax(logits))

首先用softmax将logits转换成一个概率分布，然后取概率值最大的作为样本的分类。softmax的主要作用其实是在计算交叉熵上，将logits转换成一个概率分布后再来计算，然后取概率分布中最大的作为最终的分类结果，这就是将softmax激活函数应用于多分类中。

sigmoid激活函数应用于多标签分类

sigmoid一般不用来做多类分类，而是用来做二分类，它是将一个标量数字转换到[0,1]之间，如果大于一个概率阈值(一般是0.5)，则认为属于某个类别，否则不属于某个类别。这一属性使得其适合应用于多标签分类之中，在多标签分类中，大多使用binary_cross_entropy损失函数。它是将一个标量数字转换到[0,1]之间，如果大于一个概率阈值(一般是0.5)，则认为属于某个类别。本质上其实就是针对logits中每个分类计算的结果分别作用一个sigmoid分类器，分别判定样本是否属于某个类别同样假设，神经网络模型最后的输出是这样一个向量logits=[1,2,3,4,5,6,7,8,9,10], 就是神经网络最终的全连接的输出。这里假设总共有10个分类。通过：

tf.sigmoid(logits)

sigmoid应该会将logits中每个数字都变成[0,1]之间的概率值，假设结果为[0.01, 0.05, 0.4, 0.6, 0.3, 0.1, 0.5, 0.4, 0.06, 0.8], 然后设置一个概率阈值，比如0.3，如果概率值大于0.3，则判定类别符合，那么该输入样本则会被判定为类别3、类别4、类别5、类别7及类别8。即一个样本具有多个标签。
在这里强调一点：将sigmoid激活函数应用于多标签分类时，其损失函数应设置为binary_cross_entropy(二值交叉熵见下面解释)。

binary_cross_entropy二分类交叉熵（承接上面多标签使用binary_cross_entropy损失函数）

https://www.jianshu.com/p/47172eb86b39

binary_cross_entropy是二分类的交叉熵，实际是多分类softmax_cross_entropy的一种特殊情况，当多分类中，类别只有两类时，即0或者1，即为二分类，二分类也是一个逻辑回归问题，也可以套用逻辑回归的损失函数。

1、利用softmax_cross_entropy_with_logits来计算二分类的交叉熵

来举个例子，假设一个2分类问题，假如一个batch包含两个样本，那么标签要制成二维，形如

y=[ [1, 0]，[0, 1] ]，

模型预测输出也为二维，形如

p=[ [0.8,0.2]，[0.4,0.6] ] #（softmax的输出）

那么对应的损失

L=( -log(0.8) - log(0.6) ) / 2

实际在计算中若采用softmax_cross_entropy_with_logits函数，不要事先做softmax处理。

2、套用逻辑回归代价损失函数来计算二分类的交叉熵

逻辑回归的损失函数如下：

来举个例子，假设一个2分类问题，假如一个batch包含两个样本，那么标签要制成一维，形如

y=[0，1 ]，

模型预测输出也为一维，形如

p=[ 0.2，0.6 ] #sigmoid的输出，这里一定要预先用sigmod处理，将预测结果限定在0~1之间，

那么对应的损失

L=( - 0*log(0.2) - (1 - 0)*log(1- 0.2) - log(0.6) - (1 -1)*log(1 - 0.6) ) / 2 = ( -log(0.8) - log(0.6) ) / 2

softmax_cross_entropy

以tensorflow中函数softmax_cross_entropy_with_logits为例，在二分类或者类别相互排斥多分类问题，计算 logits 和 labels 之间的 softmax 交叉熵。

数据必须经过 One-Hot Encoding 编码

tf.one_hot

用 mnist 数据举例，如果是目标值是3，那么 label 就是[0，0，0，1，0，0，0，0，0，0]，除了第4个值为1，其他全为0。

该函数把一个维度上的 labels 作为一个整体判断，结果给出整个维度的损失值。

这个函数传入的 logits 是 unscaled 的，既不做 sigmoid 也不做 softmax ，因为函数实现会在内部更高效得使用 softmax 。

softmax_cross_entropy_with_logits计算过程

1、对输入进行softmax

举个例子：假设你的输入S=[1,2,3]，那么经过softmax层后就会得到[0.09,0.24,0.67]，这三个数字表示这个样本属于第1,2,3类的概率分别是0.09,0.24,0.67。

2、计算交叉熵

L是损失，Sj是softmax的输出向量S的第j个值，前面已经介绍过了，表示的是这个样本属于第j个类别的概率。 $y_j$ 前面有个求和符号，j的范围也是1到类别数T，因此label——y是一个1*T的向量，里面的T个值，而且只有1个值是1，其他T-1个值都是0。真实标签对应的位置的那个值是1，其他都是0。所以这个公式其实有一个更简单的形式：

来举个例子吧。假设一个5分类问题，然后一个样本I的标签y=[0,0,0,1,0]，也就是说样本I的真实标签是4，假设模型预测的结果概率（softmax的输出）p=[0.1,0.15,0.05,0.6,0.1]，可以看出这个预测是对的，那么对应的损失L=-log(0.6)，也就是当这个样本经过这样的网络参数产生这样的预测p时，它的损失是-log(0.6)。那么假设p=[0.15,0.2,0.4,0.1,0.15]，这个预测结果就很离谱了，因为真实标签是4，而你觉得这个样本是4的概率只有0.1（远不如其他概率高，如果是在测试阶段，那么模型就会预测该样本属于类别3），对应损失L=-log(0.1)。

补充：sparse_softmax_cross_entropy_with_logits

sparse_softmax_cross_entropy_with_logits 是 softmax_cross_entropy_with_logits 的易用版本，除了输入参数不同，作用和算法实现都是一样的。

区别是：softmax_cross_entropy_with_logits 要求传入的 labels 是经过 one_hot encoding 的数据，而 sparse_softmax_cross_entropy_with_logits 不需要。

sigmoid_cross_entropy

以tensorflow中函数sigmoid_cross_entropy_with_logits为例说明

sigmoid_cross_entropy_with_logits函数，测量每个类别独立且不相互排斥的离散分类任务中的概率。(可以执行多标签分类，其中图片可以同时包含大象和狗。)

import tensorflow as tf

_logits = [[0.5, 0.7, 0.3], [0.8, 0.2, 0.9]]

_one_labels = tf.ones_like(_logits)

# [[1 1 1]

# [1 1 1]]

_zero_labels = tf.zeros_like(_logits)

# [[0 0 0]

# [0 0 0]]

with tf.Session() as sess:

loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=_logits, labels=_one_labels)

print(sess.run(loss))

# [[0.47407699 0.40318602 0.5543552]

# [0.37110069 0.59813887 0.34115386]]

loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=_logits, labels=_zero_labels)

print(sess.run(loss))

# [[0.97407699 1.10318601 0.85435522]

# [1.17110074 0.79813886 1.24115384]]

看看sigmoid_cross_entropy_with_logits函数定义

def sigmoid_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, name=None):

#为了描述简洁，规定 x = logits，z = labels，那么 Logistic 损失值为：

z * -log(sigmoid(x)) + (1 - z) * -log(1 - sigmoid(x))

= z * -log(1 / (1 + exp(-x))) + (1 - z) * -log(exp(-x) / (1 + exp(-x)))

= z * log(1 + exp(-x)) + (1 - z) * (-log(exp(-x)) + log(1 + exp(-x)))

= z * log(1 + exp(-x)) + (1 - z) * (x + log(1 + exp(-x))

= (1 - z) * x + log(1 + exp(-x))

= x - x * z + log(1 + exp(-x))

该函数与 softmax_cross_entropy_with_logits的区别在于：softmax_cross_entropy_with_logits中的labels 中每一维只能包含一个 1，而sigmoid_cross_entropy_with_logits中的labels 中每一维可以包含多个 1。

softmax_cross_entropy_with_logits函数把一个维度上的 labels 作为一个整体判断，结果给出整个维度的损失值，而 sigmoid_cross_entropy_with_logits 是每一个元素都有一个损失值，都是一个二分类（binary_cross_entropy）问题。