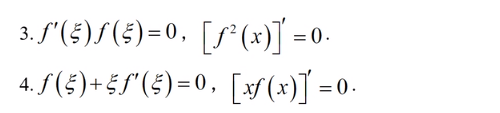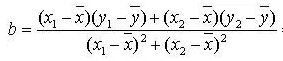目录
- 微分中值定理
- 单中值
- 一阶导数中值定理问题
- 二阶导数中值定理问题
- 双中值
- 中值不等式
- 拉格朗日证明题
- 泰勒公式证明题
- 参考资料
微分中值定理
可导 → \to → 费马 → \to → 罗尔 { 拉 氏 构 造 原 函 数 柯 西 交 叉 原 函 数 \begin{cases} 拉氏 & & {构造原函数} \\ 柯西 & & {交叉原函数} \end{cases} {拉氏柯西构造原函数交叉原函数
费马引理:设 f ( x ) f(x) f(x) 在 x 0 x_0 x0 某邻域 U ( x 0 ) U(x_0) U(x0) 内有定义,且在 x 0 x_0 x0 处可导,若 f ( x ) f(x) f(x) 在 x 0 x_0 x0 取到极值,则 f ′ ( x 0 ) = 0 f^{'}(x_0)=0 f′(x0)=0
证明:
设 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处取极大值,则 ∀ x ∈ U ( x 0 ) \forall x \in U(x_0) ∀x∈U(x0),均有 f ( x ) ≤ f ( x 0 ) f(x)≤f(x_0) f(x)≤f(x0)
又 f ( x ) f(x) f(x) 在 x 0 x_0 x0 处可导,则 f − ′ ( x 0 ) f_{-}^{'}(x_0) f−′(x0) 与 f + ′ ( x 0 ) f_{+}^{'}(x_0) f+′(x0) 都存在且相等
f − ′ ( x 0 ) = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 ≥ 0 , f + ′ ( x 0 ) = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 ≤ 0 , f_{-}^{'}(x_0) = \lim_{x \to x_{0}^{-} }\frac{ f(x) - f(x_0) }{ x-x_0 } ≥ 0, f_{+}^{'}(x_0) = \lim_{x \to x_{0}^{+} }\frac{ f(x) - f(x_0) }{ x-x_0 }≤ 0, f−′(x0)=x→x0−limx−x0f(x)−f(x0)≥0,f+′(x0)=x→x0+limx−x0f(x)−f(x0)≤0, f − ′ ( x 0 ) = f + ′ ( x 0 ) = 0 f_{-}^{'}(x_0)=f_{+}^{'}(x_0)=0 f−′(x0)=f+′(x0)=0,所以 f ′ ( x 0 ) = 0 f^{'}(x_0)=0 f′(x0)=0
罗尔定理:设 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a,b] [a,b] 连续,在开区间 ( a , b ) (a,b) (a,b) 可导,若 f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b),则 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使 f ′ ( ϵ ) = 0 f^{'}(\epsilon)=0 f′(ϵ)=0
证明:
由于 f ( x ) ∈ c [ a , b ] f(x) \in c[a,b] f(x)∈c[a,b],所以 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 存在最大值 M M M 和最小值 m m m
(1) 当 M = m M=m M=m 时, f ( x ) = M f(x)=M f(x)=M,此时 f ′ ( x ) = 0 f^{'}(x)=0 f′(x)=0,所以 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使得 f ′ ( ϵ ) = 0 f^{'}(\epsilon)=0 f′(ϵ)=0
(2) 当 M > m M>m M>m 时, 由于 f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b),则 M M M 与 m m m 至少有一个是在 ( a , b ) (a,b) (a,b) 内部取得
不妨设 M M M 在 ( a , b ) (a,b) (a,b) 内部取得,即 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使 f ( ϵ ) = M f(\epsilon)=M f(ϵ)=M,
又由于 f ( x ) f(x) f(x) 在 ϵ \epsilon ϵ 处可导且取到极大值,故 f ′ ( ϵ ) = 0 f^{'}(\epsilon)=0 f′(ϵ)=0
拉格朗日:设 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a,b] [a,b] 连续,在开区间 ( a , b ) (a,b) (a,b) 可导,则 f ( b ) − f ( a ) = f ′ ( ϵ ) ( b − a ) f(b)-f(a)=f^{'}(\epsilon)(b-a) f(b)−f(a)=f′(ϵ)(b−a)
证明:微分方程还原函数 g ( x ) = f ( x ) ( b − a ) − [ f ( b ) − f ( a ) ] x g(x)=f(x)(b-a) - [f(b)-f(a)]x g(x)=f(x)(b−a)−[f(b)−f(a)]x,
由于 g ( x ) g(x) g(x) 在 [ a , b ] [a,b] [a,b] 上连续, ( a , b ) (a,b) (a,b) 上可导, g ( a ) = g ( b ) = b f ( a ) − a f ( b ) g(a)=g(b)=bf(a)-af(b) g(a)=g(b)=bf(a)−af(b),
所以 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使 g ′ ( ϵ ) = 0 g^{'}(\epsilon)=0 g′(ϵ)=0,结论得证
柯西定理:设 F ( x ) , G ( x ) F(x), G(x) F(x),G(x) 在闭区间 [ a , b ] [a,b] [a,b] 连续,在开区间 ( a , b ) (a,b) (a,b) 可导,若 ∀ x ∈ ( a , b ) , G ′ ( x ) ≠ 0 \forall x \in (a,b), G^{'}(x)≠0 ∀x∈(a,b),G′(x)=0,则 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使 F ( b ) − F ( a ) G ( b ) − G ( a ) = F ′ ( ϵ ) G ′ ( ϵ ) \frac{F(b)-F(a)}{G(b)-G(a)}=\frac{F^{'}(\epsilon)}{G^{'}(\epsilon)} G(b)−G(a)F(b)−F(a)=G′(ϵ)F′(ϵ)
证明:交叉构造原函数 g ( x ) = F ( x ) [ f ( b ) − f ( a ) ] − f ( x ) [ F ( b ) − F ( a ) ] g(x)=F(x)[f(b)-f(a)]-f(x)[F(b)-F(a)] g(x)=F(x)[f(b)−f(a)]−f(x)[F(b)−F(a)],
由于 g ( x ) g(x) g(x) 在 [ a , b ] [a,b] [a,b] 上连续, ( a , b ) (a,b) (a,b) 上可导, g ( a ) = g ( b ) = F ( a ) f ( b ) − f ( a ) F ( b ) g(a)=g(b)=F(a)f(b)-f(a)F(b) g(a)=g(b)=F(a)f(b)−f(a)F(b),
所以 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使 g ′ ( ϵ ) = 0 g^{'}(\epsilon)=0 g′(ϵ)=0,结论得证
介值 → \to → 积分中值
积分中值:设 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上连续,则 ∃ ϵ ∈ [ a , b ] \exists \epsilon \in [a,b] ∃ϵ∈[a,b],使 ∫ a b f ( x ) d x = f ( ϵ ) ( b − a ) \int_{a}^{b}f(x)dx=f(\epsilon)(b-a) ∫abf(x)dx=f(ϵ)(b−a)
证明:因为 f ( x ) ∈ c [ a , b ] f(x) \in c[a,b] f(x)∈c[a,b],所以 ∃ m , M \exists m, M ∃m,M,使 m ≤ f ( x ) ≤ M m≤f(x)≤M m≤f(x)≤M
m ( b − a ) = ∫ a b m d x ≤ ∫ a b f ( x ) d x ≤ ∫ a b M d x = M ( b − a ) , 即 m ≤ ∫ a b f ( x ) d x b − a ≤ M m(b-a)=\int_{a}^{b}mdx≤\int_{a}^{b}f(x)dx≤\int_{a}^{b}Mdx=M(b-a),即 m≤\frac{\int_{a}^{b}f(x)dx}{b-a}≤M m(b−a)=∫abmdx≤∫abf(x)dx≤∫abMdx=M(b−a),即m≤b−a∫abf(x)dx≤M 故 ∃ ϵ ∈ [ a , b ] \exists \epsilon \in [a,b] ∃ϵ∈[a,b],使 f ( ϵ ) = ∫ a b f ( x ) d x b − a f(\epsilon)=\frac{\int_{a}^{b}f(x)dx}{b-a} f(ϵ)=b−a∫abf(x)dx,即 ∫ a b f ( x ) d x = f ( ϵ ) ( b − a ) \int_{a}^{b}f(x)dx=f(\epsilon)(b-a) ∫abf(x)dx=f(ϵ)(b−a)
拉格朗日 → \to → 积分中值推广
积分中值推广:设 f ( x ) f(x) f(x) 在 [ a , b ] [a,b] [a,b] 上连续,则 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b),使 ∫ a b f ( x ) d x = f ( ϵ ) ( b − a ) \int_{a}^{b}f(x)dx=f(\epsilon)(b-a) ∫abf(x)dx=f(ϵ)(b−a)
证明:令 F ( x ) = ∫ a x f ( t ) d t F(x)=\int_{a}^{x}f(t)dt F(x)=∫axf(t)dt, F ( x ) F(x) F(x) 在 [ a , b ] [a,b] [a,b] 上连续, ( a , b ) (a,b) (a,b) 内可导,
故 ∃ ϵ ∈ ( a , b ) \exists \epsilon \in (a,b) ∃ϵ∈(a,b), F ( b ) − F ( a ) = F ′ ( ϵ ) ( b − a ) F(b)-F(a)=F^{'}(\epsilon)(b-a) F(b)−F(a)=F′(ϵ)(b−a),即 ∫ a b f ( x ) d x = f ( ϵ ) ( b − a ) \int_{a}^{b}f(x)dx=f(\epsilon)(b-a) ∫abf(x)dx=f(ϵ)(b−a)
单中值
证明 ∃ ϵ \exist \epsilon ∃ϵ, f ( n ) ( ϵ ) = 0 f^{(n)}(\epsilon)=0 f(n)(ϵ)=0
多次罗尔定理: f ( a ) = f ( b ) = f ( c ) → f ′ ′ ( ϵ ) = 0 f(a)=f(b)=f(c) \to f^{''}(\epsilon)=0 f(a)=f(b)=f(c)→f′′(ϵ)=0
一阶导数中值定理问题
结论含 ϵ , a , b \epsilon, a, b ϵ,a,b,分离后 a , b a,b a,b,构造原函数
- 凑微分法
- 还原函数法

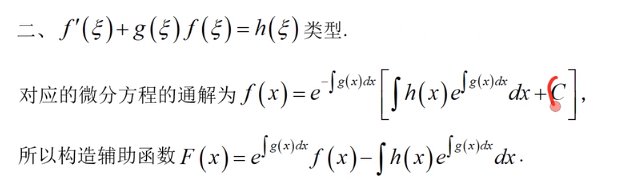
二阶导数中值定理问题
- 凑微分法



- 还原函数法 + 直接积分法



双中值
ϵ , η \epsilon,\eta ϵ,η 可能相等
ϵ , \epsilon, ϵ, 可能相等:多次在同一区间使用中值定理(拉格朗日/柯西)
分离,无 (b-a) 两次拉格朗日/柯西, ( ) ′ ( ) ′ \frac{(\quad)^{'}}{(\quad)^{'}} ()′()′ 双柯, 否则双拉,高阶导数泰勒中值

ϵ , η \epsilon,\eta ϵ,η 不可相等
ϵ , \epsilon, ϵ, 不可相等:多次在不同区间使用中值定理(临界点)
临界点:待定法强制相等 或 第1问提供




中值不等式
拉格朗日证明题



泰勒公式证明题




参考资料
【心一学长】证明题大专题
证明提大专题-中值定理(双中值)
证明题大专题-泰勒公式证明题