Chapter 1

Lesson 1

${Hint}^1：$单调函数一定有反函数。

---

$PS：$非单调的比如$y=x^2$，反过来不具有函数性质。

${Hint}^2：$任何函数都可以写成奇函数和偶函数之和。

证明：
$h(x)=f(x)+f(-x)$
$g(x)=f(x)-f(-x)$
$f(x)=h(x)+g(x)$

${Hint}^3：$${\int }_{-a}^{+a}f(x)dx={\int }_0^{+a}[f(x)+f(-x)]dx$

证明：
$${\int }_{-a}^{+a}f(x)dx={\int }_{-a}^{+a}\frac{1}{2}[f(x)+f(-x)+f(x)-f(-x)]dx$$
$$={\int }_0^{+a}[f(x)+f(-x)]dx$$
对称区间，奇函数定积分为$0$,偶函数为正区间两倍。
例： 求${\int }_{-1}^1\frac{1}{1+e^x}=?$
答案为$1$，用上面方法易得。

${Hint}^4：$分段函数和其他函数求复合函数图像或者复合函数的时候，比如$f(g(x))$，直接把$g(x)$代入到$f(x)$的分段条件中，方便计算。

Lesson 2

${Hint}^1：$如果数列收敛，那么它的极限唯一，并且一定有界。

${Hint}^2：$如果 { x n } \{x_n\} {xn​}收敛于$a$，那么它的任一子数列极限也是$a$.

---

注: 在数列 { x n } \{x_n\} {xn​}中任意抽取无限多项并保持这些项在原来数列 { x n } \{x_n\} {xn​}中的先后次序，这样得到的一个数列称为原数列 { x n } \{x_n\} {xn​}的子列。

反过来的除非是任意子数列都是$a$，才能保证收敛于$a$。

Lesson 3

${Hint}^1$：分段函数在分段点需要分左右极限/ { e ∞ → 0 / ∞ } \{e^{\infty}\to 0/\infty\} {e∞→0/∞}/ { a r c t a n ∞ → ± π 2 } \{arctan{\infty}\to \pm\frac{\pi}{2}\} {arctan∞→±2π​}

${Hint}^2$：函数极限局部有界。

${Hint}^3$：极限大于$0$，说明存在一个去心邻域，$f(x)>0$

${Hint}^4$：$$\underset{x\to x_0}{\lim }f(x)=(\underset{x_n\to x_0}{\lim }f(x_n))=\underset{n\to \infty }{\lim }f(x_n)[\underset{n\to \infty }{\lim }{x}_n=x_0]=A$$

Lesson 4

${Hint}^1$：

$1)$有限个无穷小的和仍是无穷小。
$2)$有界函数与无穷小的乘积仍是无穷小。$$\underset{x\to \infty }{\lim }\frac{sinx}{x}=无穷小\ast 有界函数=0$$
$3)$有限个无穷小的积仍是无穷小。

${Hint}^2$：

$1)$无穷大要求邻域内每个数都大于任意一个值。
$2)$无界要求存在一个数大于任意一个值。

${Hint}^3$:

在自变量的同一变化过程中，如果$f(x)$为无穷大，那么$\frac{1}{f(x)}$为无穷小；反之，如果$f(x)$为无穷小，且$f(x)\ne 0$，那么$\frac{1}{f(x)}$为无穷大。
例：
$y=xcosx$是否有界，是否是$x\to +\infty$的无穷大$?$
取$x=2k\pi$,$y=2k\pi >\forall M$
所以$y=xcosx$在$(-\infty ,+\infty )$上无界
取$x=2k\pi +\frac{\pi }{2}$，$y=0$.所以当$x\to \infty$不是无穷大。

${Hint}^4$：已知$\lim c_n$不存在，$\lim b_n$存在且不等于$0$，能否判断$\lim b_n{c}_n$是否存在[这里$x$都趋近于$\infty$]？

首先$f(x)=1[x\in R]$,$\lim f(x)=1$,且$\lim b_n$存在且不等于$0$
根据极限运算法则，$\lim \frac{1}{b_n}$存在。
假设$\lim b_n{c}_n$存在，则有$\lim c_n=\lim b_n{c}_n\ast \lim \frac{1}{b_n}$存在。
与条件不符，所以$\lim b_n{c}_n$不存在。

${Hint}^5$：数列极限找反例的时候，可以试试

$(-1{)}^{n}n\to \infty$
$\frac{1}{n}\to 0$
$\frac{n}{n+1}\to 1$

Lesson 6

本节知识点一共两个：
两个极限存在准则，两个重要极限。

${Hint}^1$：夹逼准则

如果数列$x_n,y_n,z_n$满足以下条件：
$1)$从某项起，即$\exists N>0$，当$n>N$时，有$x_n\le y_n\le z_n$
$2)$$\underset{n\to \infty }{\lim }{x}_n=\underset{n\to \infty }{\lim }{z}_n=a$,则数列$y_n$有极限，且$\underset{n\to \infty }{\lim }{y}_n=a$
例：$\underset{x\to 0^{+}}{\lim }x[\frac{1}{x}]$
解：
$\frac{1}{x}-1\le [\frac{1}{x}]\le \frac{1}{x}$
当$x\to 0^{+}$，则$x$是整数，则有：$1-x\le x[\frac{1}{x}]\le 1$
显然根据夹逼准则，左右极限是$1$，答案是$1$

${Hint}^2$：证明一个重要极限 $\underset{x\to 0}{\lim }\frac{sin}{x}=1$

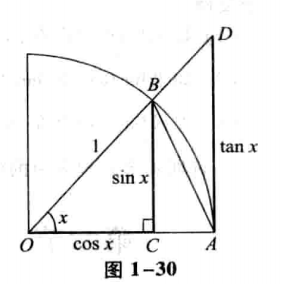
容易发现：
$S三角形AOB=\frac{1}{2}sinx<S扇形AOB=\frac{1}{2}x<SAOD=\frac{1}{2}tanx$
则有：
$$sinx<x<tanx$$
$$1<\frac{x}{sinx}<\frac{1}{cosx}$$
$$cosx<\frac{sinx}{x}<1$$
用$-x$替换的时候，我们发现等式不变，也就是在$(-\frac{\pi }{2},\frac{\pi }{2})$都成立。
根据夹逼准则，左右极限都是$1$，所以$\underset{x\to 0}{\lim }\frac{sinx}{x}=1$

${Hint}^3$：一些等价无穷小

$tanx\sim x$
$1-cosx\sim \frac{1}{2}{x}^2$
$arcsinx\sim x$

${Hint}^4$：理解一下换元法对反三角函数的重要性

求：$\underset{x\to 0}{\lim }\frac{arcsinx}{x}$
解：
令$t=arcsinx$，则$x=sint$，当$x\to 0$时，$t\to 0$。
于是由复合函数的极限运算法则得：
$\underset{x\to 0}{\lim }\frac{arcsinx}{x}=\underset{t\to 0}{\lim }\frac{t}{sint}=1$

${Hint}^5$：单调有界准则(则有极限)

若数列$x_n$单调增加， 且有上界，则极限$\underset{n\to \infty }{\lim }{x}_n$存在。
反之，单减，且有下界，则有极限存在。

---

$PS:$ 如果在$x_0$的左邻域有界单调，则存在左极限$f(x_0^{-})$。右极限同理。

${Hint}^6$：收敛的函数一定有界，有界的数列不一定收敛。

${Hint}^7$：另一个重要极限$\underset{x\to \infty }{\lim }(1+\frac{1}{x}{)}^x=e$或$\underset{x\to 0}{\lim }{(1+x)}^{\frac{1}{x}}=e$

---

$PS:$即$(1+\to 0{)}^{\to \infty }=1^{\infty }$

${Hint}^8$：幂指函数极限预算法则：$\underset{x\to x_0}{\lim }{(f(x)\to A)}^{g(x)\to B}=A^B$

---

前提是两个极限都存在。

${Hint}^9$：优先凑极限，而不是优先替换等价无穷小之类的。

$\underset{x\to 0}{\lim }(1+2x{)}^{\frac{3}{sinx}}=\underset{x\to 0}{\lim }{(1+2x)}^{\frac{1}{2x}\ast \frac{6x}{sinx}}=\underset{x\to 0}{\lim }[(1+2x{)}^{\frac{1}{2x}}{]}^{\frac{6sinx}{x}}=e^6$

${Hint}^{10}$：理解数学归纳法在求单调有界准则上的妙用以及利用两边极限列方程。

数学归纳法源于假设，当你需要证明某个东西，却缺少某个结论，但是你猜测这个结论是正确的时候，你可以使用数学归纳法尝试去证明。
数学归纳法：初值满足结论，假设第$k$个满足结论，求证$k+1$也满足。

例：数列$\sqrt{2}，\sqrt{2+\sqrt{2}}，\sqrt{2+\sqrt{2+\sqrt{2}}}，...$的极限存在。
解：
（盲猜单调，利用单调有界证明

$x_{k+1}=\sqrt{x_k+2}$
$x_{k+1}-x_k=\sqrt{x_k+2}-x_k=\frac{x_k+2-x_k^2}{\sqrt{x_k+2}+x_k}=\frac{(2-x_k)(1+x_k)}{\sqrt{x_k+2}+x_k}$

（可以猜测$x_k$单增，也就是需要$x_k<2$，即可证明单增。

由$x_1=\sqrt{2}<2$，假设$x_k<2$，则$x_{k+1}=\sqrt{x_k+2}<\sqrt{2+2}=2$
则证明$x_n<2(n=1,2,3,...,n)$，即有上界，同时也证明了单增。
根据单调有界即可证明极限存在

如果要求极限呢？
令$\underset{n\to \infty }{\lim }{x}_n=A$，$x_{n+1}=\sqrt{2+x_n}$，两边极限，列方程。
$A=\sqrt{2+A}$,且$A>0$，得出$A=2$.

Lesson 7

${Hint}^1$：等价无穷小具有自反性、对称性、传递性。

${Hint}^2$：无穷小证明，注意$\underset{x\to 0}{\lim }\frac{o(x^m)}{x^m}=0$

1)
$o(x^2)+o(x^2)=o(x^2)$
$\underset{x\to 0}{\lim }\frac{o(x^2)\pm o(x^2)}{x^2}=\underset{x\to 0}{\lim }\frac{o(x^2)}{x^2}\pm \underset{x\to 0}{\lim }\frac{o(x^2)}{x^2}=0$
是比$x^2$的高阶无穷小。所以正确。
2)
$o(x^2)\pm o(x^3)=o(x^2)$
$\underset{x\to 0}{\lim }\frac{o(x^2)\pm o(x^3)}{x^2}=\underset{x\to 0}{\lim }\frac{o(x^2)}{x^2}+\underset{x\to 0}{\lim }\frac{o(x^3)}{x^3}\ast x=0$
正确。
3
$o(2x^2)=o(x^2)$
$\underset{x\to 0}{\lim }\frac{o(2x^2)}{x^2}=\underset{x\to 0}{\lim }\frac{o(2x^2)}{2x^2}\ast 2=2\ast 0=0$
正确。

$Hin{t}^3$：无穷小的有关基本定理

定理一：$\beta \sim \alpha \iff \beta =\alpha +o(\alpha )$
比如说：
$x\to 0$时，$x^3+3x\sim 3x$
1)
$\underset{x\to 0}{\lim }\frac{x^3+3x}{3x}=\underset{x\to 0}{\lim }\frac{x^2}{3}+1=1$
说明了等价无穷小。
2)
$x^3+3x=3x+o(3x)$
说明了等价无穷小。
定理二： 若$\alpha \sim {\alpha }_1$，$\beta \sim {\beta }_1$，则$\lim \frac{\beta }{\alpha }=\lim \frac{{\beta }_1}{{\alpha }_1}$

${Hint}^4$：等价无穷小们

$x\to 0$时，
$sinx\sim arctanx\sim tanx\sim arctanx\sim \ln (1+x)\sim e^x-1\sim x$
$1-cosx\sim \frac{1}{2}{x}^2$，$(1+\alpha x{)}^{\beta }-1=\alpha \beta x$，$a^x-1\sim xlna$

${Hint}^5$：

1、体会一下极限中的有理化过程。
2、以及在得到常数极限相乘的情况，可直接提出来【整体式子的系数才行】。
例：
$求\underset{x\to 0}{\lim }\frac{\sqrt{1+\tan x}-\sqrt{1+\sin x}}{x\sqrt{1+{\sin }^{2}x}-x}$
解：
$I=\underset{x\to 0}{\lim }\frac{\tan x-\sin x}{x(\sqrt{1+{\sin }^{2}x-1})}\ast \frac{1}{\sqrt{1+\tan x}+\sqrt{1+\sin x}}$(无理化转换为有理化)
$=\frac{1}{2}\underset{x\to 0}{\lim }\frac{\tan x-\sin x}{x(\sqrt{1+{\sin }^{2}x}-1)}$(提出来常数乘着的极限)
$=\frac{1}{2}\underset{x\to 0}{\lim }\frac{\tan x(1-\cos x)}{x(\frac{1}{2}{\sin }^{2}x)}$
$=\frac{1}{2}\underset{x\to 0}{\lim }\frac{x\ast \frac{1}{2}{x}^2}{x\ast \frac{1}{2}{x}^2}=\frac{1}{2}$
3、提取公因数从而转换成等价无穷小里的$1/$或者转换成$x$
例：
$求\underset{x\to 0}{\lim }\frac{e^{\tan x}-e^{\sin x}}{x^3}$
解：
$I=\underset{x\to 0}{\lim }\frac{e^{\sin x}(e^{\tan x-\sin x}-1)}{x^3}$(为了转换成$e^x-1$，从而把某个数提出来)
$=\underset{x\to 0}{\lim }\frac{\tan x-\sin x}{x^3}$
$=\underset{x\to 0}{\lim }\frac{\tan x(1-\cos x)}{x^3}$
$=\underset{x\to 0}{\lim }\frac{1-\cos x}{x^2}=\frac{1}{2}$