Chapter 3

Lesson 1

${Hint}^1$：微分中值定理——联系函数和导数

费马引理：对于邻域$U(x_0)$，如果对于$f(x)\le f(x_0)$(或$f(x)\ge f(x_0)$ )，那么$f^{\prime }(x_0)=0$
罗尔定理：
1、在闭区间$[a,b]$上连续
2、在开区间$(a,b)$内可导
3、在区间端点处的函数值相等，即$f(a)=f(b)$，那么在$(a,b)$内至少一个点 $x$,$f^{\prime }(x)=0$

$PS:$
验证有根 : 零点定理和罗尔定理

${Hint}^2$：拉格朗日中值定理——联系函数和导数

如果函数$f(x)$满足：
1、在闭区间$[a,b]$上连续
2、在开区间$(a,b)$内可导
那么在$(a,b)$内至少有一点$x$,使$f(b)-f(a)=f^{\prime }(x)(b-a)$

${Hint}^3$：

证明 $x>0$ 时，$\frac{x}{1+x}<\ln (x+1)<x$
证明:
令 $f(x)=\ln (1+x)$在$[0,x]$上，则$f(x)-f(0)=x{f}^{\prime }(\delta )$
则，$\ln (1+x)=\frac{1}{1+\delta }x$，$\delta \in (0,x)$
所以，得证。
$PS:$
1、遇到$f(b)-f(a)$
2、把$f$和导数联系

${Hint}^4$：柯西中值定理

如果$f(x)$或$F(x)$满足
1、在区间$[a,b]$上连续
2、在开区间可导
3、对任一$x$∈$(a,b)$，$F^{\prime }(x)!=0$
则存在一点$\delta \in (a,b)$，使$\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f^{\prime }(\delta )}{F^{\prime }(\delta )}$
$PS:$
一般$F$是具体函数，$f$是抽象的

Lesson 2

${Hint}^1$：

洛必达法则：
1、$\frac{0}{0}$或者$\frac{\infty }{\infty }$
2、在去心邻域内，$f^{\prime }(x)$及$F^{\prime }(x)$都存在，且$F^{\prime }(x)\ne 0$
3、求导后的极限存在，或者无穷大
$PS:$
求导后的极限可以得到原来的极限。
但是从原来的极限，不能得到求导后的极限。
例如：
$\underset{x\to \infty }{\lim }\frac{x+\sin x}{x}=\lim (1+\cos x)$
求导后的极限振荡不存在，不能使用洛必达法则。
例：
$\underset{x\to +\infty }{\lim }\frac{\ln x}{n{x}^n}=0$
$\underset{x\to +\infty }{\lim }\frac{x^n}{e^{\lambda x}}=\underset{x\to +\infty }{\lim }\frac{n!}{{\lambda }^n{e}^{\lambda x}}=0$
综上所述，则有$x\to +\infty ,\ln x<<x^n<<e^{\lambda x}(n>0,\lambda >0)$
$\underset{x\to 0^{+}}{\lim }{x}^n\ln x=\underset{x\to 0^{+}}{\lim }\frac{\ln x}{\frac{1}{x^n}}=0$
$\underset{x\to \frac{\pi }{2}}{\lim }\sec x-\tan x=\underset{x\to \frac{\pi }{2}}{\lim }(\frac{1}{\cos x}-\frac{\sin x}{\cos x})=0$
$PS:$
$0\ast \infty$变成$0\ast 0$或者$\infty \ast \infty$，需要把对数和反三角函数作为分子，否则过于麻烦

${Hint}^2$：幂指函数求极限$f(x{)}^{g(x)}=e^{g(x)\ln f(x)}$

$0^0:$$\underset{x\to 0}{\lim }{x}^x=e^0=1$
${\infty }^0:$$\underset{x\to 0^{+}}{\lim }(\frac{1}{x}{)}^{\tan x}=e^0=1$
$1^{\infty }:$$\underset{x\to +\infty }{\lim }(\frac{2}{\pi }\arctan x{)}^x=e^{-\frac{2}{\pi }}$洛必达；
用凑重要极限也可以，最终要 求:$\lim (\arctan x-\frac{\pi }{2})x=-1$
这里

Lesson 3

${Hint}^1$：

$f(x)=f(x_0)+\sum \frac{f^{\prime }(x_0)}{k!}(x-x_0{)}^k+o((x-x_0{)}^n)$
$f(x)=a_0+a_1(x-x_0)+...+a_k(x-x_0{)}^k+...+a_n(x-x_0{)}^n+o((x-x_0{)}^n)$
最后$o$是佩亚诺余项$=\frac{f^{n+1}(\delta )}{(n+1)!}(x-x_0{)}^{n+1}$

1、若取$x_0=0$，则上述泰勒公式称为麦克劳林公式
2、泰勒公式具有唯一性：$f^{(n)}(x_0)=a_n\ast n!$ 则利用这个可以求高阶导

Lesson 4

${Hint}^1$：函数单调增加：$f^{\prime }(x)>0$，除了最多有限个点($f^{\prime }(x)=0$或$f^{\prime }(x)不\exists$)

注意：
只有驻点和不可导点才能成为单调区间的分界点

${Hint}^2$:

恒有$f(\frac{x_1+x_2}{2})>\frac{f(x_1)+f(x_2)}{2}$，则是凸的
$f(x_0)+f^{\prime }(x_0)(x-x_0)>f(x)$凸的
$f^{\prime \prime }(x)<0$ 凸的

${Hint}^3$:

拐点$(x_0,f(x_0))$是连续函数凹凸分界点。
若是拐点，则$f^{\prime \prime }(x_0)=0$或者不存在。

判断方法一：

1. f’’(x)在两侧变号，则是拐点
2. f’’(x)不变号，则不是

判断方法二：

1. $f^{\prime \prime \prime }(x_0)\ne 0$则是。
2. 如果$f^{\prime \prime }(x_0)=0$，则不确定。

${Hint}^3$:

不过太神了，还可以求导或者拉格朗日中值定理(容易证)。

Lesson 5

${Hint}^1$:

1、 极值点 $=>f^{\prime }(x_0)=0$或不存在
2、二阶导不为$0$，则$x_0$是极值点，$>0$是极小值点。[]
3、极值点了两侧导数变号

${Hint}^2$:

函数和各式导数联系在一起，则可以想到泰勒公式

${Hint}^3$:

${Hint}^3$:

绝对值函数的分界点不可导
连续函数时，若极值点唯一，则其必然是最值(简单思考：易证)

Lesson 6

${Hint}^1$:

1、铅直渐近线：

2、水平渐近线：

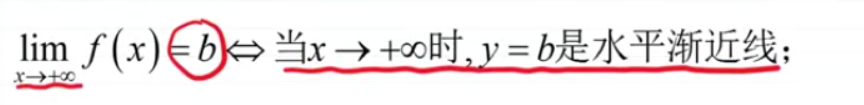
3、斜渐近线：

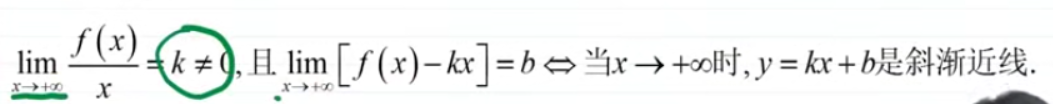
$2$和$3$在同一侧不共存。

${Hint}^2$: