python3
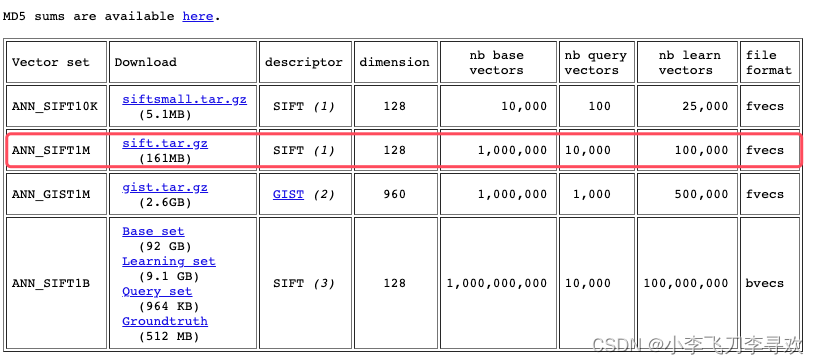
dirsearch 暴力扫描网页结构(包括网页中的目录和文件)
下载地址:https://gitee.com/xiaozhu2022/dirsearch/repository/archive/master.zip
下载解压后,在dirsearch.py文件窗口,打开终端(任务栏cmd 或 右击打开快捷菜单)
使用方法:
安装:pip install dirsearch
使用:diresearch -u http://example.com/ -e *
-u:url
-e:扩展名列表,用逗号隔开(例如:php,asp)
查看返回值,大部分都是503,返回200的表示可以访问

![[足式机器人]Part3机构运动微分几何学分析与综合Ch03-1 空间约束曲线与约束曲面微分几何学——【读书笔记】](https://img-blog.csdnimg.cn/303488597c624fe0b2cb55cbc3532adc.png)