当下海外游戏市场仍然具备较大的增长空间。据机构预测，至2025年全球移动游戏市场规模将达1606亿美元，对应2020-2025年复合增长率11％。与此同时，随着元宇宙概念持续升温，国内外多家互联网巨头纷纷入场。行业分析平台Newzoo发布2022年游戏行业趋势报告曾预测：“元宇宙”之火将持续掀起游戏赛道激烈竞争态势。

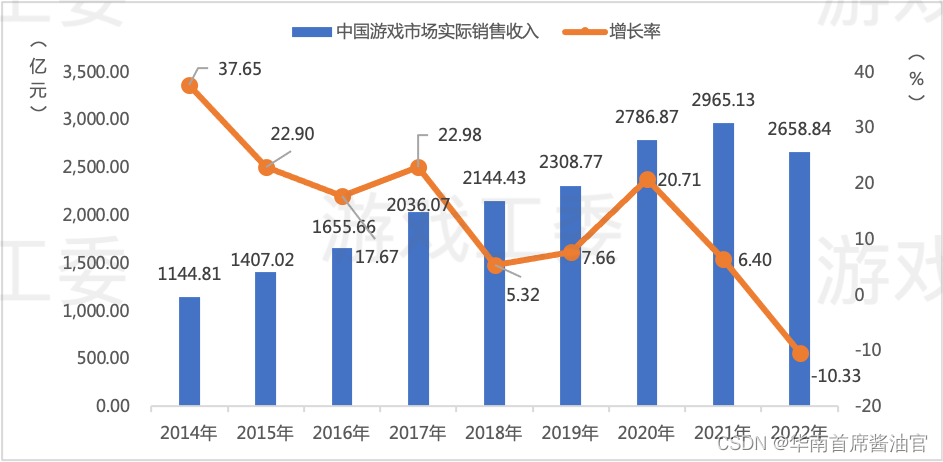
 今年以来，国内网络游戏市场面临较大压力，据伽马数据最新发布《2022 年第三季度（7-9 月）游戏产业报告》显示，中国游戏市场在去年实际销售收入597.03亿元，环比下降12.61%，同比下降19.13%。但凭借多年精品化游戏战略，至2023年，本阶段实现逆势增长，和数软件旗下UTONMOS多款长线元宇宙游戏产品，包括《神念无界-源起山海》、《北荒传奇》、《神宠岛》、《北荒战纪》等屡创行业新高。另外，UTONMOS海外元宇宙游戏市场也早已打开布局，长线运营的精品优势进一步显现。

 在自我迭代迅猛的游戏行业，当元宇宙赛道加速破圈，游戏“出海”如何抓住新风口？业内指出，虚实相生的技术带来更多联动效应，需重构产业上下游关系，增强不同领域和行业跨界融合，放大数据和用户连通的全新价值空间。一批国内外企业纷纷聚焦自身优势领域，拓展生态版图。业内认为，元宇宙能够在虚实融合、以虚促实中推动虚拟经济与实体经济融合发展，赋能驱动千行百业新市场、新业态、新模式的发展。

 和数软件在多个关键技术和应用场景上有所突破，重点聚焦和数链BaaS平台、文化创意、数字IP、数字医疗、链游戏、硬件生态、元宇宙场景应用等多个方向展开布局，在科技和文化领域构建产生长期发展的价值基石。