C语言练习7
- 编程题
前言
“芳林新叶催陈叶,流水前波让后波。”改革开放40年来,我们以敢闯敢干的勇气和自我革新的担当,闯出了一条新路、好路,实现了从“赶上时代”到“引领时代”的伟大跨越。今天,我们要不忘初心、牢记使命,继续以逢山开路、遇水架桥的开拓精神,开新局于伟大的社会革命,强体魄于伟大的自我革命,在我们广袤的国土上继续书写13亿多中国人民伟大奋斗的历史新篇章!
编程题
一,输入一个整数,将这个整数以字符串的形式逆序输出,程序不考虑负数的情况,若数字含有0,则逆序形式也含有0,如输入为100,则输出为001。
数据范围: 1 <= n <= 2^30 - 1
输入描述:输入一个int整数。
输出描述:将这个整数以字符串的形式逆序输出。
OJ链接【牛客网题号: HJ11 数字颠倒】【难度:简单】
示例:
输入:1516000
输出:0006151
💡分析:
这道题只需要循环取出一个数字的每一位进行单独打印,打印完毕后换行即可。而获取数据的每一位,可以通过取每次对数字模和除以 10 来完成
🔑 代码实现
//HJ11 数字颠倒
int main()
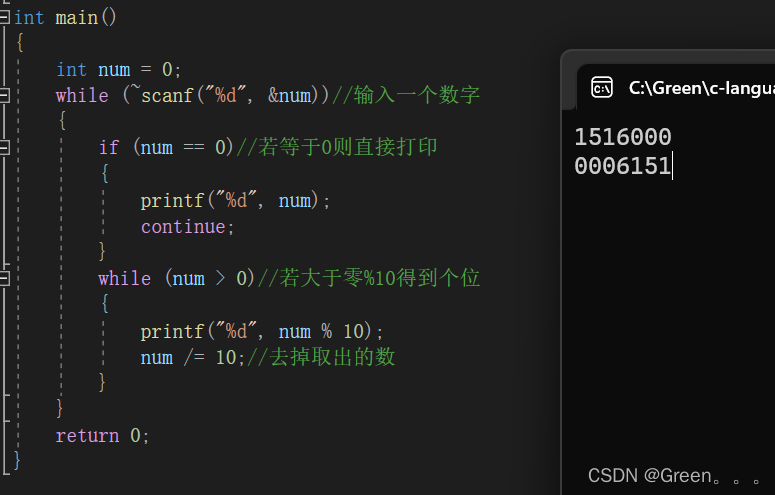
{int num = 0;while (~scanf("%d", &num))//输入一个数字{if (num == 0)//若等于0则直接打印{printf("%d", num);continue;}while (num > 0)//若大于零%10得到个位{printf("%d", num % 10);num /= 10;//去掉取出的数}}return 0;
}
💯运行结果:
二,对字符串中的所有单词进行倒排。
说明:
1、构成单词的字符只有26个大写或小写英文字母;
2、非构成单词的字符均视为单词间隔符;
3、要求倒排后的单词间隔符以一个空格表示;如果原字符串中相邻单词间有多个间隔符时,倒排转换后也只
允许出现一个空格间隔符;
4、每个单词最长20个字母;
OJ链接【牛客网题号: HJ31 单词倒排】【难度:简单】
示例:
输入:I am a student
输出:student a am I
💡分析:
这道题的解题思路不难,定义一个字符指针数组,用于保存每个单词的起始字符地址,接下来将非字母字符全部替换成为字符串结尾标志,则单词字符字母遇到结尾就结束了,相当于把一个字符串以非字母字符进行切割成为了多个字符串,最终对字符指针数组进行逆序打印每个单词即可。
🔑 代码实现
#include <stdio.h>
#include <string.h>
//HJ31 单词倒排
int main()
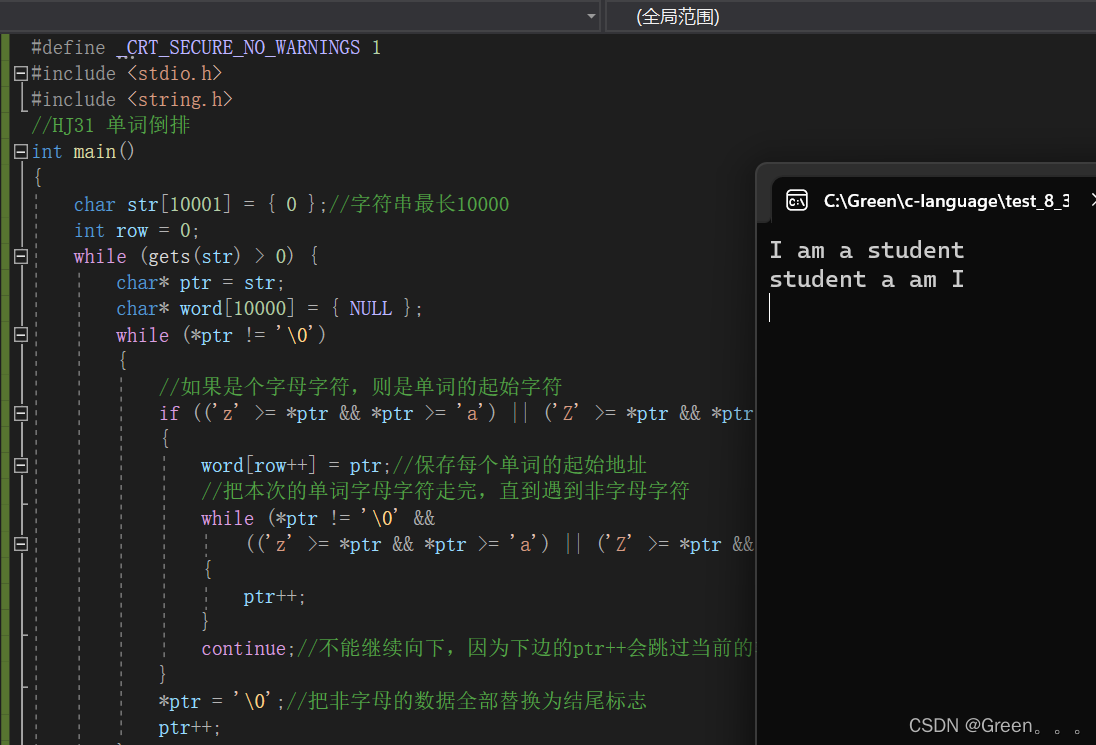
{char str[10001] = { 0 };//字符串最长10000int row = 0;while (gets(str) > 0) {char* ptr = str;char* word[10000] = { NULL };while (*ptr != '\0') {//如果是个字母字符,则是单词的起始字符if (('z' >= *ptr && *ptr >= 'a') || ('Z' >= *ptr && *ptr >= 'A')) {word[row++] = ptr;//保存每个单词的起始地址//把本次的单词字母字符走完,直到遇到非字母字符while (*ptr != '\0' &&(('z' >= *ptr && *ptr >= 'a') || ('Z' >= *ptr && *ptr >= 'A'))) {ptr++;}continue;//不能继续向下,因为下边的ptr++会跳过当前的非字母字符}*ptr = '\0';//把非字母的数据全部替换为结尾标志ptr++;}for (int i = row - 1; i >= 0; i--){printf("%s ", word[i]);//针对所有单词的起始地址逆序开始打印即可}printf("\n");}
}
💯运行结果:
三,1、给定一个二进制数组, 计算其中最大连续 1 的个数。
leetcode【 leetcode 题号:485. 最大连续 1 的个数】【难度:简单】
示例:
输入:[1,1,0,1,1,1]
输出:3
解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3
💡分析:
这道题思路比较简单,统计连续1的个数,遇到0时表示连续中断,判断如果当前的统计数大于之前最大的则替换,然后继续下一个位置开始的统计即可。
🔑 代码实现
int findMaxConsecutiveOnes(int* nums, int numsSize)
{int max_count = 0;int cur_count = 0;int i = 0;for (i = 0; i < numsSize; i++){if (nums[i] == 1){cur_count++;}else{max_count = max_count > cur_count ? max_count : cur_count;cur_count = 0;}}max_count = max_count > cur_count ? max_count : cur_count;return max_count;
}
四,求输出n以内(含n)完全数的个数。完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。
例如:28,它有约数1、2、4、7、14、28,除去它本身28外,其余5个数相加,1+2+4+7+14=28。
注意:本题输入含有多组样例。
输入描述:输入一个数字n
输出描述:输出不超过n的完全数的个数
OJ链接【牛客网题号: HJ56 完全数计算】【难度:简单】
示例:
输入:1000 7 100
输出:3 1 2
💡分析:
🔑 代码实现
int is_perfect_num(int num)
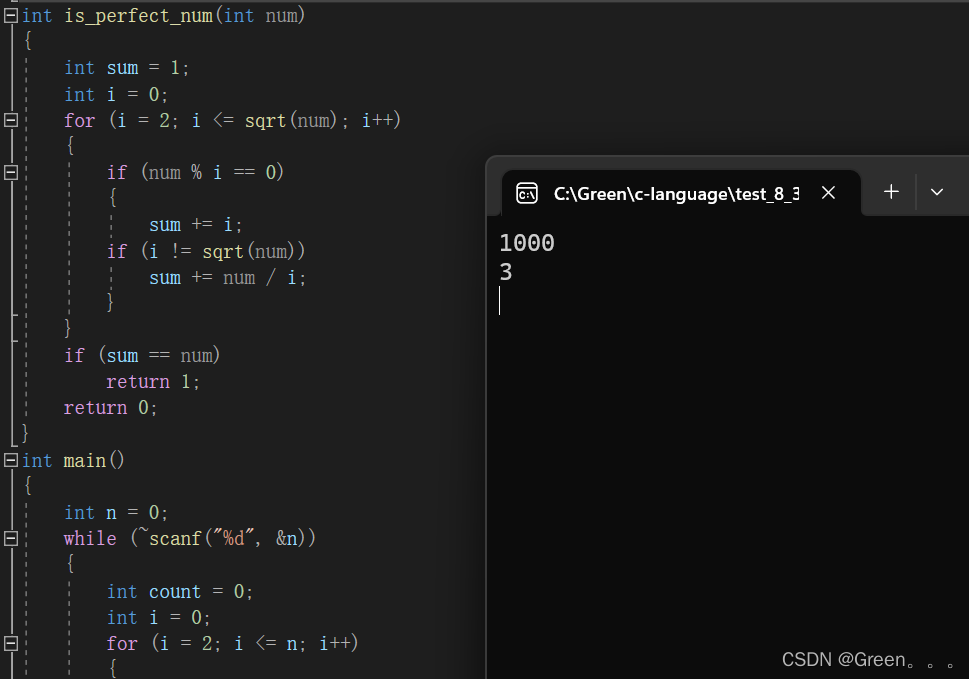
{int sum = 1;int i = 0;for (i = 2; i <= sqrt(num); i++){if (num % i == 0){sum += i;if (i != sqrt(num))sum += num / i;}}if (sum == num)return 1;return 0;
}
int main()
{int n = 0;while (~scanf("%d", &n)){int count = 0;int i = 0;for (i = 2; i <= n; i++){if (is_perfect_num(i)){count++;}}printf("%d\n", count);}return 0;
}
💯运行结果:
五,给你一个含 n 个整数的数组 numvs ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出
现在 nums 中的数字,并以数组的形式返回结果。
leetcode【 leetcode 题号:448. 找到所有数组中消失的数字】【难度:简单】
示例:
输入:nums = [4,3,2,7,8,2,3,1]
输出:[5,6]
输入:nums = [1,1]
输出:[2]
💡分析:
numsSize 大小的数组,其中每个元素的数据在 [1, numsSize] 区间之内,解法其实并不复杂,以数组元素的绝对值作为下标,将对应位置的数据置为负数,比如 0 号位置是 3 ,则把 3 号位置的数据重置为负值,等到数组遍历重置完毕,只有缺失的这个数字对应的位置保留正数,其他出现过的数字位置都会是负数, 要注意不要重复设置负数,因为负负得正。
示例:
[2, 3, 3, 2, 4] 注意数组10个元素,值为[1-10], 但是访问下标应该在[0-9]之内,因此修改位置下标应该是值-1
0号元素是2,则将1号位置置为对应负值 [2, -3, 3, 2, 4]
1号元素是3,则将2号位置置为对应负值 [2, -3, -3, 2, 4]
2号元素是-3,绝对值为3,将2号位置为负值,但是2号位已经重置过,不需要重置,否则会变正数[2, -3, -3, 2, 4]
3号元素是-2,绝对值为2,将1号位置为负值,但是1号位已经重置过,不需要重置,否则会变正数[2, -3, -3, 2, 4]
4号元素是4,则将3号位置置为对应负值 [2, -3, -3, -2, 4]
遍历数组得到0,4两个位置的数据是大于0的,因为人家数值从1开始,因此+1后得到1, 5两个缺失的数字
🔑 代码实现
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize)
{for (int i = 0; i < numsSize; i++){if (nums[abs(nums[i]) - 1] > 0)nums[abs(nums[i]) - 1] = -(nums[abs(nums[i]) - 1]);}int* ret = (int*)malloc(sizeof(int) * (numsSize));*returnSize = 0;for (int i = 0; i < numsSize; i++){if (nums[i] > 0) {ret[*returnSize] = i + 1;*returnSize += 1;}}return ret;
}
六,写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
数据范围:两个数都满足 0≤n≤1000
OJ链接【牛客网题号: JZ65 不用加减乘除做加法】【难度:简单】
示例:
输入:1,2
返回值:3
💡分析:
十进制相加思想: 15+07 , 先计算不考虑进位的相加结果 12 (因为 5+7 的不考虑进位的结果是 2 ,遇 10 进位嘛),然后计算进位 5+7 进位是 10 ,则 10 与 12 再次相加,得到 22 ,进位为 0 ,则计算到此结束。
这里使用二进制求和完成,思想类似,但是二进制计算相加和进位不需要使用 + 符号
二进制相加思想:与十进制相同,先计算不考虑进位的相加结果( 0+0 得 0 , 1+1 进位得 0 , 1+0 得 1 ),使用异或可以取得; 然后计算相加的进位结果(同 1 的位置左移一位即可),使用相与后左移取得。
示例:
5 0101 + 7 0111
不考虑进位的相加结果 0101^0111 -> 0010
相加的进位 0101&0111 -> 0101 因为进位左移得到 1010
1010 + 0010
不考虑进位的相加结果 1010 ^ 0010 -> 1000
相加的进位 1010 & 0010 -> 0010 因为进位左移得到 0100
1000 + 0100
不考虑进位的相加结果 1000 ^ 0100 -> 1100
相加的进位 1000 & 0100 -> 0000 进位为0结束运算
🔑 代码实现
int Add(int num1, int num2)
{while (num2 != 0) {//进位不为0则持续与相加结果进行相加int tmp = num1 ^ num2;//得到每位相加不考虑进位的数据num2 = (num1 & num2) << 1;//同1的位相加则会进位num1 = tmp;}return num1;
}
七,给你一个长度为 n 的整数数组 nums ,其中 n > 1 ,返回输出数组 output ,其中 output[i] 等于 nums 中除nums[i] 之外其余各元素的乘积。
提示:题目数据保证数组之中任意元素的全部前缀元素和后缀(甚至是整个数组)的乘积都在 32 位整数范围内。
leetcode【 leetcode 题号:238. 除自身以外数组的乘积】【难度:中等】
示例:
输入: [1,2,3,4]
输出: [24,12,8,6]
💡分析:
🔑 代码实现
int Add(int num1, int num2)
{while (num2 != 0) {//进位不为0则持续与相加结果进行相加int tmp = num1 ^ num2;//得到每位相加不考虑进位的数据num2 = (num1 & num2) << 1;//同1的位相加则会进位num1 = tmp;}return num1;
}
八,自除数 是指可以被它包含的每一位数除尽的数。例如, 128 是一个自除数,因为 128 % 1 == 0 , 128 % 2 ==0 , 128 % 8 == 0 。还有,自除数不允许包含 0 。给定上边界和下边界数字,输出一个列表,列表的元素是边界(含边界)内所有的自除数。
leetcode【 leetcode 题号:728. 自除数】【难度:简单】
示例:
输入:上边界left = 1, 下边界right = 22
输出: [1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 15, 22]
💡分析:
暴力不考虑其他的因素的话,将所有数据乘积起来,然后遍历数组除以当前位置数据即可。
更优解法:将乘积分为两次进行,第一次先将每个位置左边的数据乘积计算出来放到返回数组中,后边第二次循环将对应位置右边的数据乘积计算出来与返回数组对应位置的左半边乘积相乘得到结果。
示例: 一个数组 int nums[ ] = {2, 3, 4} 。
int left = 1, right = 1;
计算左侧乘积:
第0个元素的左边乘积, arr[0] = left 然后计算第1位左侧乘积 left*=nums[0] -> left = 12
第1个元素的左边乘积, arr[1] = left 然后计算第2位左侧乘积 left=nums[1] -> left = 123
第2个元素的左边乘积, arr[2] = left 然后计算第3位左侧乘积 已经没必要了,因为第2元素是末尾元素了
一次循环完毕后,返回数组中每个元素存储的都是自己左侧元素的乘积。 arr[]中的值: [1, 2, 6]
计算右侧乘积:
第2个元素的右边乘积, arr[2] = right 然后计算第1位右侧乘积 right=nums[2] -> right =14
第1个元素的右边乘积, arr[1] = right 然后计算第0位右侧乘积 right=nums[1] -> right =143
第0个元素的右边乘积, arr[0] = right 然后计算第-1位右侧乘积 -1位已经不需要计算了
循环完毕后,返回数组中的每个元素都是其他元素的乘积了 arr[2]=1; arr[1]=4; arr[0]*=12
🔑 代码实现
int* selfDividingNumbers(int left, int right, int* returnSize)
{int* ret = (int*)calloc(1000, sizeof(int));//动态申请足够大的空间用于存放返回的自除数*returnSize = 0;for (int i = left; i <= right; i++) {int num = i;while (num) {int remainder = num % 10;//计算余数if (remainder == 0 || (i % remainder) != 0) {//判断i自身与余数取模是否为0break;}num /= 10;}//如果num==0表示通过了每一位数的取模判断,则i就是自除数if (num == 0) ret[(*returnSize)++] = i;}return ret;
}
💘后期会推出更多C语言练习题,希望大家与我共同进步,早日成为大佬!