LeetCode-64. 最小路径和【数组 动态规划 矩阵】
- 题目描述:
- 解题思路一:动态规划五部曲。定推初遍举
- 解题思路二:动态规划优化空间,直接改grid
- 解题思路三:dfs
题目描述:
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
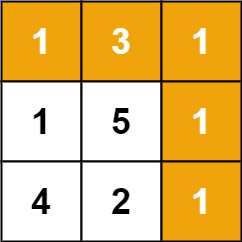
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200
此题解法与LeetCode-62. 不同路径【数学 动态规划 组合数学】非常相似!
解题思路一:动态规划五部曲。定推初遍举
-
确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从左上角出发到 (i,j) 位置的最小路径和。 -
确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)的最小路径和,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
- dp数组的初始化
如何初始化呢,首先dp[0][0] = grid[0][0],从(0, 0)的位置到(i, 0)的路径就是相加即可,那么dp[0][j]也同理。
dp[0][0] = grid[0][0]
for i in range(1, m):dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, n):dp[0][j] = dp[0][j-1] + grid[0][j]
- 确定遍历顺序
这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。
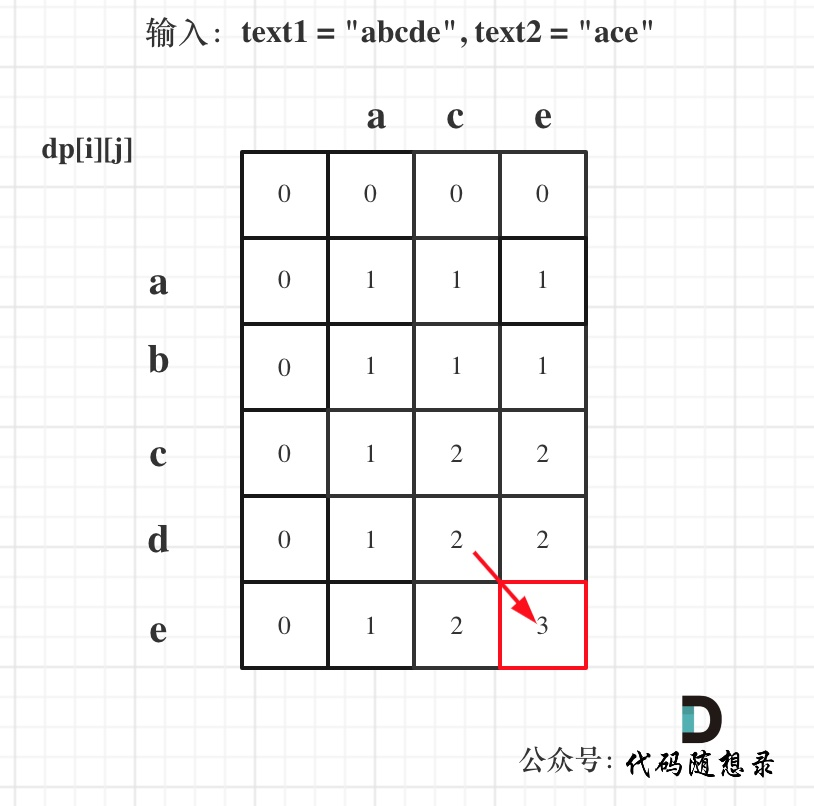
- 举例推导dp数组
如图所示:
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])dp = [[0] * n for _ in range(m)]dp[0][0] = grid[0][0]for i in range(1, m):dp[i][0] = dp[i-1][0] + grid[i][0]for j in range(1, n):dp[0][j] = dp[0][j-1] + grid[0][j]for i in range(1, m):for j in range(1, n):dp[i][j] = min(grid[i][j] + dp[i-1][j], grid[i][j] + dp[i][j-1])return dp[-1][-1]
时间复杂度:O(nm)
空间复杂度:O(nm)
解题思路二:动态规划优化空间,直接改grid
class Solution:def minPathSum(self, grid: [[int]]) -> int:for i in range(len(grid)):for j in range(len(grid[0])):if i == j == 0: continueelif i == 0: grid[i][j] = grid[i][j - 1] + grid[i][j]elif j == 0: grid[i][j] = grid[i - 1][j] + grid[i][j]else: grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j]return grid[-1][-1]
时间复杂度:O(nm)
空间复杂度:O(1)
解题思路三:dfs
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:m, n = len(grid), len(grid[0])@cachedef dfs(m,n):if m==0 and n ==0:return grid[m][n]if m==0:return dfs(m,n-1)+grid[m][n]if n==0:return dfs(m-1,n)+grid[m][n]return min(dfs(m-1,n),dfs(m,n-1))+grid[m][n]return dfs(m-1,n-1)
时间复杂度:O(nm)
空间复杂度:O(nm)