思路
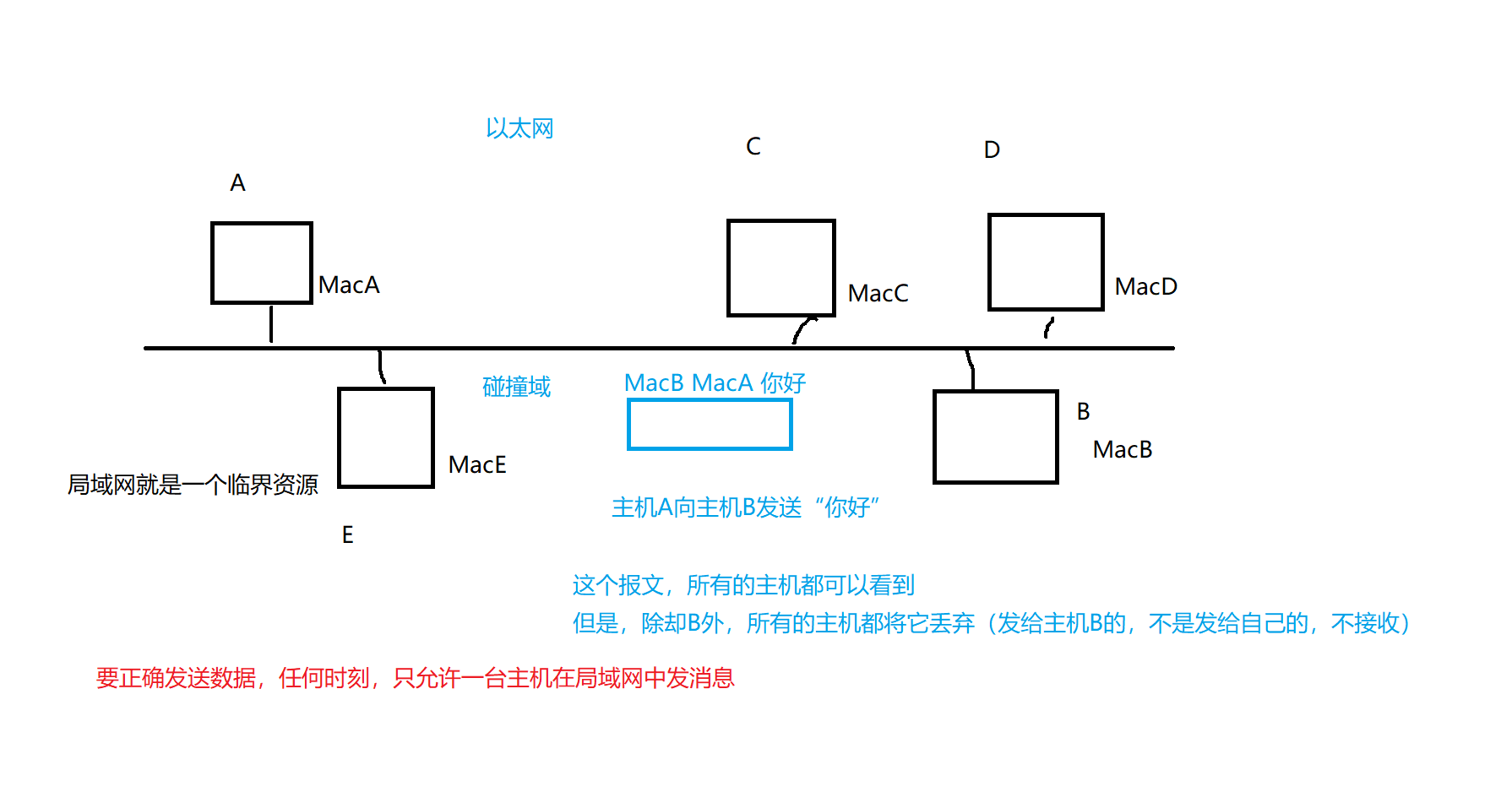
考虑到题目中的规则,每个印章图案的边必须和网格图边重合,网格图上的每一个格子最多只能被一个印章图案覆盖,印章的图案在网格图上必须是完整的。这意味着每个印章图案都会覆盖一个独立的、完整的区域,且这些区域不会相互重叠。
设第一种印章覆盖的格子数为 x x x,第二种印章覆盖的格子数为 y y y,那么它们的总覆盖格子数为 c n t = x + y cnt = x + y cnt=x+y。同时,题目给出两种印章的使用次数之和为 k k k。由于每种印章的使用次数必须是整数,我们可以设第一种印章的使用次数为 a a a,第二种印章的使用次数为 b b b,那么 a + b = k a + b = k a+b=k。又有 3 a + 2 b = c n t 3a + 2b = cnt 3a+2b=cnt。
这两个方程构成一个线性方程组,可以使用消元法求解。先将第二个方程乘以2得到 2 a + 2 b = 2 k 2a + 2b = 2k 2a+2b=2k,然后将第一个方程减去这个得到 a = c n t − 2 k a = cnt - 2k a=cnt−2k。这就是印章A的使用次数。
接着,将求得的印章A的使用次数 a a a 代入第二个方程 a + b = k a + b = k a+b=k,可以解得 b = k − a = 3 k − c n t b = k - a = 3k - cnt b=k−a=3k−cnt。这就是印章B的使用次数。
首先从输入中读取三个整数 n、m 和 k,这三个整数分别表示网格图的行数、列数和两种印章的使用次数之和。然后,通过一个循环,读取 n × m n \times m n×m 个字符,每个字符表示一个网格图上的格子,字符 ‘1’ 表示这个位置被印章图案覆盖,字符 ‘0’ 表示这个位置没有被覆盖。在读取每个字符的同时,如果字符为 ‘1’,则将计数器 cnt 加一,这样 cnt 就表示了印章覆盖的格子总数。
在读取完所有字符之后,输出两种印章的使用次数。第一种印章的使用次数为 (cnt - 2 * k),第二种印章的使用次数为 (3 * k - cnt)。这样就得到了每种印章的使用次数。
AC代码
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;const int N = 1e6 + 7;
const int INF = 0x3f3f3f3f;ll n, m, k;
ll cnt = 0;int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m >> k;for (int i = 1; i <= n * m; i++) {char t;cin >> t;cnt += (t == '1');}cout << (cnt - 2 * k) << " " << (3 * k - cnt) << "\n";return 0;
}