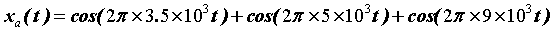matlab学习005-利用matlab设计滤波器

一，含有多个频率成分的三角信号

1，以采样频率fs=20KHz对信号采样，画出信号的波形；

1）前期基础

2）波形图

3）代码

2，选取合适的采样点数，利用DFT分析信号的频谱，并画出信号幅度频谱图；

1）前期基础

2）频谱图

3）代码

3，设计一个滤波器，滤除信号中频率为9KHz的分量；画出滤波器的频响特性曲线；

1）前期基础

2）特性曲线

☀

3）代码

4，用设计的滤波器对信号进行滤波，画出滤波器的输出信号的波形和幅度频谱图。

1）前期基础

2）效果

3）代码

二，周期性方波信号

1，产生一个周期为0.001秒，幅值为±1的方波信号，画出信号的时域波形（画4个周期）

1）前期基础

2）时域波形图

3）代码

2，选择合适的采样频率，用MATLAB画出该信号波形；

1）前期基础

2）时域波形图

3）代码

3，选取合适的采样点数，利用DFT分析该周期信号的频谱，并画出幅度频谱图；

1）前期基础

2）幅度频谱图

3）代码

4，设计一个滤波器，滤除该信号中三次谐波及以上的频率成分，画出滤波器的频响特性曲线；

1）前期基础

2）频响特性曲线

3）代码

5，用设计的滤波器对信号滤波，画出滤波器的输出信号的时域波形和幅度频谱图。

1）前期基础

2）滤波后信号的时域波形和幅度频谱图

3）代码

一，含有多个频率成分的三角信号

设有连续信号：

【xa(t)=cos(2Π*3.5*10^3t)+cos(2Π*5*10^3t)+cos(2Π*9*10^3t)】

1，以采样频率fs=20KHz对信号采样，画出信号的波形；

1）前期基础

①相关公式：

Δf=1/(N*Ts)=1/T=fs/N;
Ts=1/fs；

②对应名称：

Ts：采样周期（采样时间间隔）
T：时域采样时间长度（采样前模拟信号的时间长度）（采样时间是指完成一组样本的采集所需要的时间）
Δf：频率分辨率
N：采样点数
fs：采样频率

③需要注意：

对固定时间长度 (T) 的信号，采集到过大的数据量即采样点数 (N=T/△t)，会给计算机增加不必要的计算量和存储空间。
若采样点数(N) 限定，则采样时间过短，会导致一些数据信息被排斥在外。
若采样频率过低，采样点间隔过远，则离散信号不足以反映原有信号波形特征，无法使信号复原造成信号混叠。

④步骤：

1）首先定义信号中的三个频率成分（也可以不定义，直接在表达式中写），当频率成分比较大且多时，还是推荐将不同的频率成分预先定义出来，在代码编写时，就会一目了然且简洁明了许多。

2）接着确定采样频率。题目已经给出了采样频率fs为=20kHz。如果题目没有给，就需要自己去求，可以根据（nyquist）奈奎斯特抽样定理来确定采样频率：fs>=2fh（待采样信号的最高频率）。

        ①观察xa信号，可以看到，信号的最大模拟角频率Ω(或称ω)：ω=2Π*9*10^3。

        ②根据公式：fh=1/T(min)=1 /2Π / ω(max)= ω(max) / 2Π ，可得fh=9*10^3=9e3（计算器或电脑表达10的幂是一般是用E或e，即e3表示1000）。

        ③因为fs>=2fh=2*9e3=18e3(Hz) ，所以，fs最小只能取18kHz ，可以是19kHz，也可以是20kHz，21kHz等。由于题目要求fs就是20kHz，因此令fs=2e4就行。

3）接着，计算采样时间间隔 Ts。

  根据以前高中学过的知识：周期等于频率的倒数T=1/f。同样可以类推得到采样周期Ts（采样时间间隔）的公式：Ts=1/fs（采样频率）=1/20000=0.00005（这个结果不用真的算出来，写好等式，放到程序里面，让计算机来算）。

4）之后创建一个时间向量 t。

        该时间向量t用一个区间来表示：起始时间位置:Ts:终止时间位置。相应的时间位置可以是从 0 到 0.1 秒的时间段，也可以是从 0 到 0.01 秒的时间段，在实际应用中，可根据自己的需求调整时间范围。时间变量t是以采样时间间隔 Ts （采样周期）为步长。

5）然后，我就可以根据这个时间向量t来生成信号 xa。

6）最后，调用 plot 函数来绘制信号的波形图。针对本文中的xa信号，我选择了 0.009 秒的时间范围。

2）波形图

绘制出的波形图如下：

如果时间向量t = 0:Ts:1-Ts; 那么绘制出来的波形图将会如下：

将图片放大之后：

3）代码

% 定义信号参数  
f1 = 3.5e3; % 第一个频率分量  
f2 = 5e3;   % 第二个频率分量  
f3 = 9e3;   % 第三个频率分量  % 定义采样频率  
fs = 20e3; % 采样频率，单位 Hz  % 计算采样时间间隔  
Ts = 1/fs; % 采样时间间隔，单位s  % 定义时间向量，比如取 0.009 s的时间范围  
t = 0:Ts:0.009-Ts; % 生成时间向量  % 根据时间向量生成信号  
xa = cos(2*pi*f1*t) + cos(2*pi*f2*t) + cos(2*pi*f3*t);  % 使用 MATLAB 画图  
plot(t, xa); % 绘制信号波形  
xlabel('时间t/s'); % x轴标签  
ylabel('信号幅度f/dB'); % y轴标签  
title('cos(2*pi*f1*t) + cos(2*pi*f2*t) + cos(2*pi*f3*t)的信号波形图'); % 图形标题  
grid on; % 显示网格

2，选取合适的采样点数，利用DFT分析信号的频谱，并画出信号幅度频谱图；

1）前期基础

确定采样频率和采样点数：
- 采样频率（fs）必须满足采样定理，即fs > 2 * fh，其中fh是信号中的最高频率成分。
- 采样点数（N）应该足够大，以便在频率域中有足够的分辨率。
采样信号：
- 使用上述确定的采样频率对信号进行采样。
计算DFT：
- 调用fft函数，对采样后的信号执行DFT运算。
- 需要注意的是：fft函数返回的是复数结果，其中包含了幅度和相位信息。因此需要通过abs函数，来提取这些复数的幅度。
- 由于DFT的结果是对称的（对于实数输入信号），因此我只需要绘制一半的频率范围。
绘制幅度频谱图：
- 计算DFT结果的幅度。
- 绘制幅度与频率的关系图。
- 在绘制时，需要对幅度进行归一化，并且乘以2，以补偿只取了一半频率范围的事实。

最后使用plot函数绘制出幅度与频率的信号幅度频谱图，如下👇

2）频谱图

3）代码

% 定义信号参数  
f1 = 3.5e3; % 第一个频率分量  
f2 = 5e3;   % 第二个频率分量  
f3 = 9e3;   % 第三个频率分量  
fs = 2e4; % 采样频率，题目给定且满足采样定理  
Ts = 1/fs; % 采样周期  
t = 0:Ts:1-Ts; % 时间向量  % 定义信号  
xa = cos(2*pi*f1*t) + cos(2*pi*f2*t) + cos(2*pi*f3*t);  % 计算DFT  
N = length(xa); % 得到xa信号的采样点数  
X = fft(xa); %  使用函数fft，执行DFT运算  % 计算频率轴（频率分辨率Δf=fs/N）  
df = fs*(0:(N/2))/N; % 只取一半，因为DFT是对称的  % 计算幅度频谱  
amplitude = abs(X(1:N/2+1)); % 取幅度并只取一半（不包括直流分量）  % 绘制幅度频谱图  
plot(df, 2*amplitude/N); % 归一化幅度并乘以2（因为只取了半边）  
title('xa的信号幅度谱');  
xlabel('频率/Hz');  
ylabel('幅度/dB'); 
grid on;

3，设计一个滤波器，滤除信号中频率为9KHz的分量；画出滤波器的频响特性曲线；

1）前期基础

①选择合适的滤波器类型

要设计一个滤波器来滤除信号中频率为9kHz的分量，首先我需要明确滤波器的设计目标，然后选择一个合适的滤波器类型。

②调用滤波器相关函数

在MATLAB中，可以使用内置的滤波器设计函数来设计滤波器，并使用频率响应函数来绘制滤波器的频响特性曲线。

③绘制其频响特性曲线的步骤

1）对于本问题，可以选择设计一个带阻滤波器（Band-stop Filter）或者一个陷波滤波器（Notch Filter），专门用来抑制特定频率分量。考虑到采样频率fs=20kHz，我们需要确保滤波器设计不会违背采样定理，即滤波器的截止频率应低于fs/2，也就是10kHz，以避免混叠效应。

2）推荐使用巴特沃斯（Butterworth）滤波器作为带阻滤波器的类型，也可以根据自己的需求选择其他类型的滤波器，比如椭圆滤波器（Elliptic）或切比雪夫滤波器（Chebyshev），这些滤波器类型提供了不同的通带和阻带特性。

①buttord函数用于计算所需的最小滤波器阶数和截止频率。

②butter函数用于设计巴特沃斯滤波器。

③freqz函数用于计算滤波器的频率响应，并且我们将其转换为实际的频率值进行绘图

3）最后用plot函数绘制幅度响应曲线，这里是以分贝（dB）为单位的。

在本文中，所绘制的图形及给定参数都仅供参考，有些地方需要根据自己的具体需求进行调整。

特别是滤波器参数（如通带和阻带的边缘频率、衰减等）需要仔细选择以达到最佳效果。

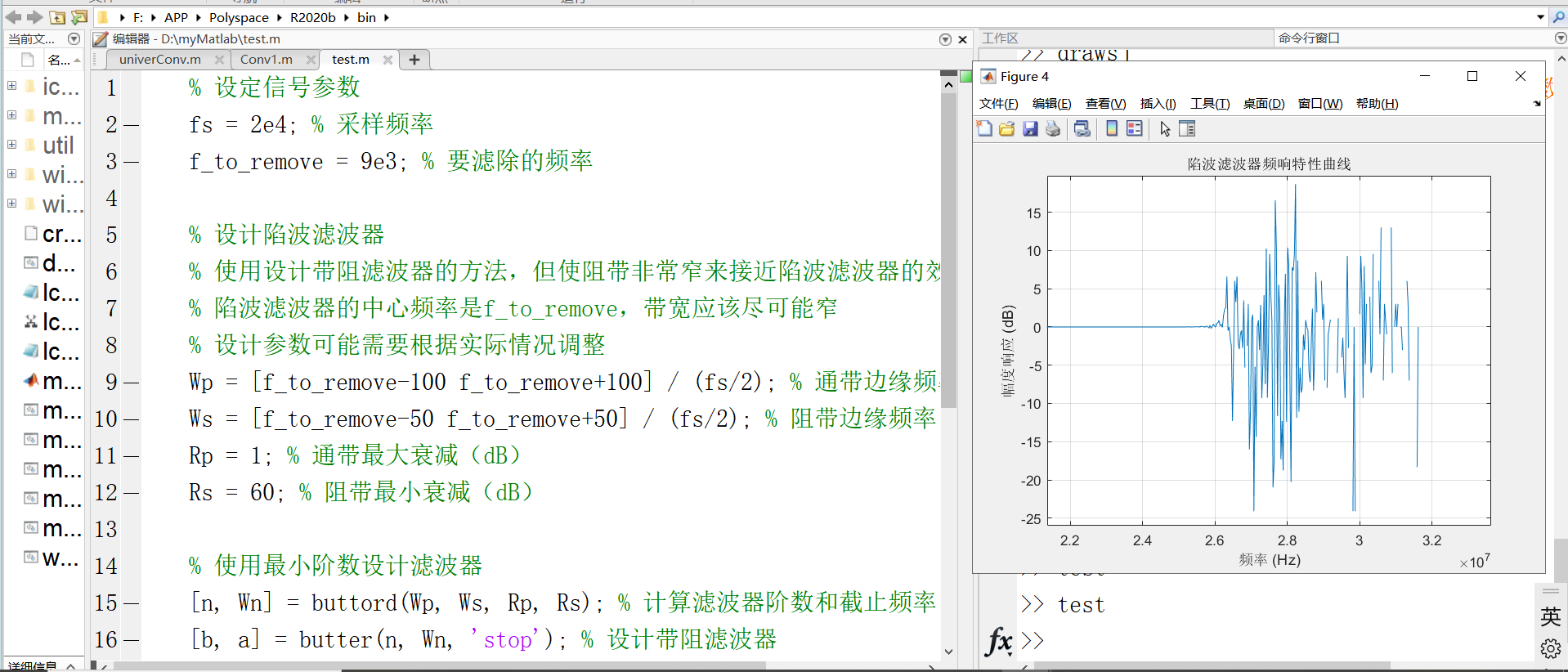
以下是一个使用MATLAB设计陷波滤波器的特性曲线及代码。

2）特性曲线

3）代码

% 设定信号参数  
fs = 2e4; % 采样频率  
f_to_remove = 9e3; % 要滤除的频率  % 设计陷波滤波器  
% 使用设计带阻滤波器的方法，但使阻带非常窄来接近陷波滤波器的效果  
% 陷波滤波器的中心频率是f_to_remove，带宽应该尽可能窄  
% 设计参数可能需要根据实际情况调整  
Wp = [f_to_remove-100 f_to_remove+100] / (fs/2); % 通带边缘频率（归一化）  
Ws = [f_to_remove-50 f_to_remove+50] / (fs/2); % 阻带边缘频率（归一化）  
Rp = 1; % 通带最大衰减（dB）  
Rs = 60; % 阻带最小衰减（dB）  % 使用最小阶数设计滤波器  
[n, Wn] = buttord(Wp, Ws, Rp, Rs); % 计算滤波器阶数和截止频率  
[b, a] = butter(n, Wn, 'stop'); % 设计带阻滤波器  % 绘制滤波器的频响特性曲线  
[h, w] = freqz(b, a, 1024, fs); % 计算频率响应  % 绘制滤波器频率响应  
figure;  
plot(w/pi*fs/2, 20*log10(abs(h))); % 转换为实际频率并绘制幅度响应（dB）  
grid on;  
title('陷波滤波器频响特性曲线');  
xlabel('频率 (Hz)');  
ylabel('幅度响应 (dB)');  
axis([2.5 fs/2 -100 10]); % 限制x轴范围为0到采样频率的一半

4，用设计的滤波器对信号进行滤波，画出滤波器的输出信号的波形和幅度频谱图。

1）前期基础

①步骤

定义信号参数和采样频率。
创建一个包含所需频率成分的信号。
设计一个带阻滤波器或陷波滤波器，以滤除9kHz的频率分量。
应用滤波器到信号上。
绘制滤波后信号的波形和幅度频谱图。

②注意点

iirnotch函数可以用来设计陷波滤波器，该函数需要两个参数：陷波频率（归一化到0和1之间）和滤波器带宽（陷波深度）。带宽参数可能需要调整以获得最佳性能。
可以根据实际情况调整滤波器的设计参数以获得最佳效果。还需要考虑滤波器的阶数，以平衡过渡带宽和滤波器陡度之间的权衡。

2）效果

3）代码

% 定义信号参数  
f1 = 3.5e3; % 3.5 kHz  
f2 = 5e3;   % 5 kHz  
f3 = 9e3;   % 9 kHz  
fs = 2e4;   % 采样频率 20 kHz  
Ts=1/fs;    % 采样时间间隔
t = 0:Ts:1-Ts; % 时间向量  % 创建信号  
xa = cos(2*pi*f1*t) + cos(2*pi*f2*t) + cos(2*pi*f3*t);  % 设计一个IIR带阻滤波器，或者使用FIR滤波器（根据需求选择）
[b, a] = iirnotch(f3/(fs/2), 0.5); % iirnotch函数用于设计陷波滤波器  % 应用滤波器  
filterx = filter(b, a, xa);   % filterx是经过滤波器滤波后的信号 % 绘制滤波后信号的波形  
figure;  
subplot(2,1,1);  
plot(t, filterx);  
title('滤波后信号的波形');  
xlabel('时间/s');  
ylabel('幅度/dB');  % 计算并绘制滤波后信号的幅度频谱  
X= fft(filterx);  % X是滤波后的信号filterx使用fft函数，经过dft运算的信号
amplitude= abs(X/length(X));  % 幅度
amplitude(2:end-1) = 2*amplitude(2:end-1);  
y= fs*(0:(length(X)/2))/length(X);  subplot(2,1,2);  
plot(y, amplitude(1:length(X)/2+1))   
title('滤波后信号的幅度频谱');  
xlabel('频率/Hz');  
ylabel('幅度/dB');

二，周期性方波信号

1，产生一个周期为0.001秒，幅值为±1的方波信号，画出信号的时域波形（画4个周期）

1）前期基础

步骤

首先创建并定义时间轴，使该时间轴覆盖至少包含4个周期的时间点。
接着定义方波的周期和要绘制的周期数。
然后使用MATLAB的square函数生成方波信号创建一个方波信号，其幅值为±1，周期为0.001秒。
之后使用plot函数绘制方波信号的时域波形，并添加网格、轴标签和标题
最后使用xlim和ylim函数来设置x轴和y轴的范围，以确保所有重要的信息都包含在图形中。

2）时域波形图

3）代码

% 定义参数  
T = 0.001; % 周期  
N_cycles = 4; % 周期数  
t = 0:T/1000:N_cycles*T; % 时间轴，以足够小的步长覆盖4个周期  % 创建方波信号  
A = 1; % 幅值  
square_wave = A * square(2*pi*t/T); % MATLAB的square函数生成方波  % 绘制时域波形  
figure; % 创建一个新的图形窗口  
plot(t, square_wave); % 绘制方波信号  
grid on; % 打开网格  
xlabel('时间/s'); % x轴标签  
ylabel('幅度/dB'); % y轴标签  
title('显示4个周期的方波信号'); % 图形标题  
xlim([0 N_cycles*T]); % 设置x轴范围以显示4个周期  
ylim([-A*1.1 A*1.1]); % 设置y轴范围以包含所有幅值

2，选择合适的采样频率，用MATLAB画出该信号波形；

1）前期基础

要选择合适的采样频率以绘制方波信号波形，我需要确保采样定理（Nyquist-Shannon定理）得到满足。采样定理指出，为了无失真地重建原始信号，采样频率fs必须至少是信号最高频率分量fh的两倍。

对于方波信号，其最高频率分量fh是基频f0的奇数次谐波。
对于理想的方波，其最高频率分量fh是无穷大的，但在实际应用中，我们通常关注其前几次谐波。

对于周期为0.001秒的方波信号，其基频f0=1/0.001 = 1000 Hz。如果我只关心到某个特定的谐波次数，比如5次或7次，那么最高频率分量将是5f0或7f0。为了确保信号被正确采样，采样频率fs应该至少是这个最高频率分量的两倍。

这里，我选择一个较高的采样频率，比如基频的10倍，即10 kHz。这样，即使考虑到一些高频分量，也能保证信号的准确采样。

绘制其时域波形图及代码如下👇：

2）时域波形图

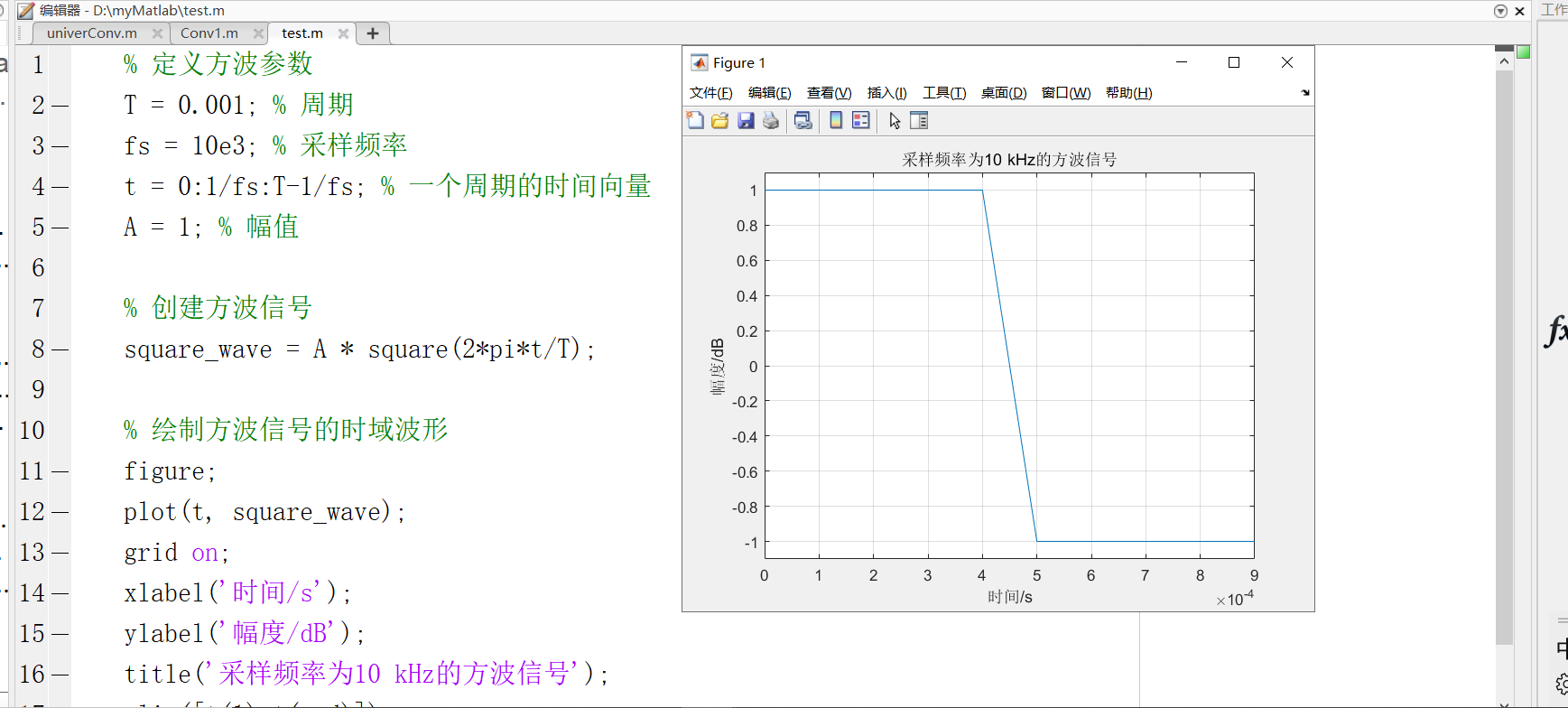
如上创建了一个时间向量t，它只包含一个周期的时间点。

3）代码

% 定义方波参数  
T = 0.001; % 周期  
fs = 10e3; % 采样频率  
t = 0:1/fs:T-1/fs; % 一个周期的时间向量  
A = 1; % 幅值  % 创建方波信号  
square_wave = A * square(2*pi*t/T);  % 绘制方波信号的时域波形  
figure;  
plot(t, square_wave);  
grid on;    
xlabel('时间/s');  
ylabel('幅度/dB');  
title('采样频率为10kHz的方波信号'); 
xlim([t(1) t(end)]);  
ylim([-A*1.1 A*1.1]);

由于方波是周期性的，可以通过复制这个波形来展示多个周期。要绘制多个周期的波形，可以做以下修改：

t要包含4个周期的时间点
使用mod函数用于确保在每个周期结束时信号重新开始，这对于绘制周期性信号非常有用。
然后，绘制在这个扩展时间向量上的方波信号。

代码如下：

% 定义方波参数  
Ts = 0.001; % 周期  
fs = 10e3; % 采样频率  
n_cycles = 4; % 要绘制的周期数  
t = 0:1/fs:n_cycles*Ts-1/fs; % 多个周期的时间向量  
A = 1; % 幅值  % 创建方波信号  
square_wave = A * square(2*pi*mod(t, Ts)/Ts); % 使用mod确保周期性  % 绘制方波信号的时域波形  
figure;  
plot(t, square_wave);  
grid on;  
xlabel('时间/s');  
ylabel('幅度/dB');  
title('采样频率为10kHz的方波信号(4个周期)');  
xlim([t(1) t(end)]);  
ylim([-A*1.1 A*1.1]);

覆盖四个周期的方波信号波形图如下👇

3，选取合适的采样点数，利用DFT分析该周期信号的频谱，并画出幅度频谱图；

1）前期基础

①选取合适的采样点数

为了使用DFT（离散傅里叶变换）分析周期信号的频谱，并绘制其幅度频谱图，需要首先选择合适的采样点数。通常，采样点数应该选择为2的幂次，以便能够利用FFT（快速傅里叶变换）算法高效地计算DFT。

对于方波信号，由于它的频谱包含多个谐波分量，我们需要选择足够多的采样点数来捕获这些分量。采样点数N至少应该大于等于信号中最高频率分量fh的两倍（即N>=2fh），选择更多的采样点数可以获取更平滑的频谱图。

下面是一个MATLAB脚本，它使用FFT计算方波信号的频谱，并绘制幅度频谱图：

②步骤

首先定义方波信号的参数，
创建包含4个周期的时间向量和对应的方波信号。
然后，使用fft函数计算信号的FFT，
创建了一个频率向量f，它对应于FFT结果中的每个点。
接着，计算幅度频谱P2，并对正频率部分进行处理，且FFT的结果是对称的。
最后，使用plot函数绘制幅度频谱图。

③注意点

由于方波信号的频谱包含许多高频分量，因此即使使用了很多采样点，幅度频谱图仍然可能会显得比较“嘈杂”。
在实际应用中，可以通过窗口函数（如Hamming窗或Hanning窗）来平滑频谱图。

2）幅度频谱图

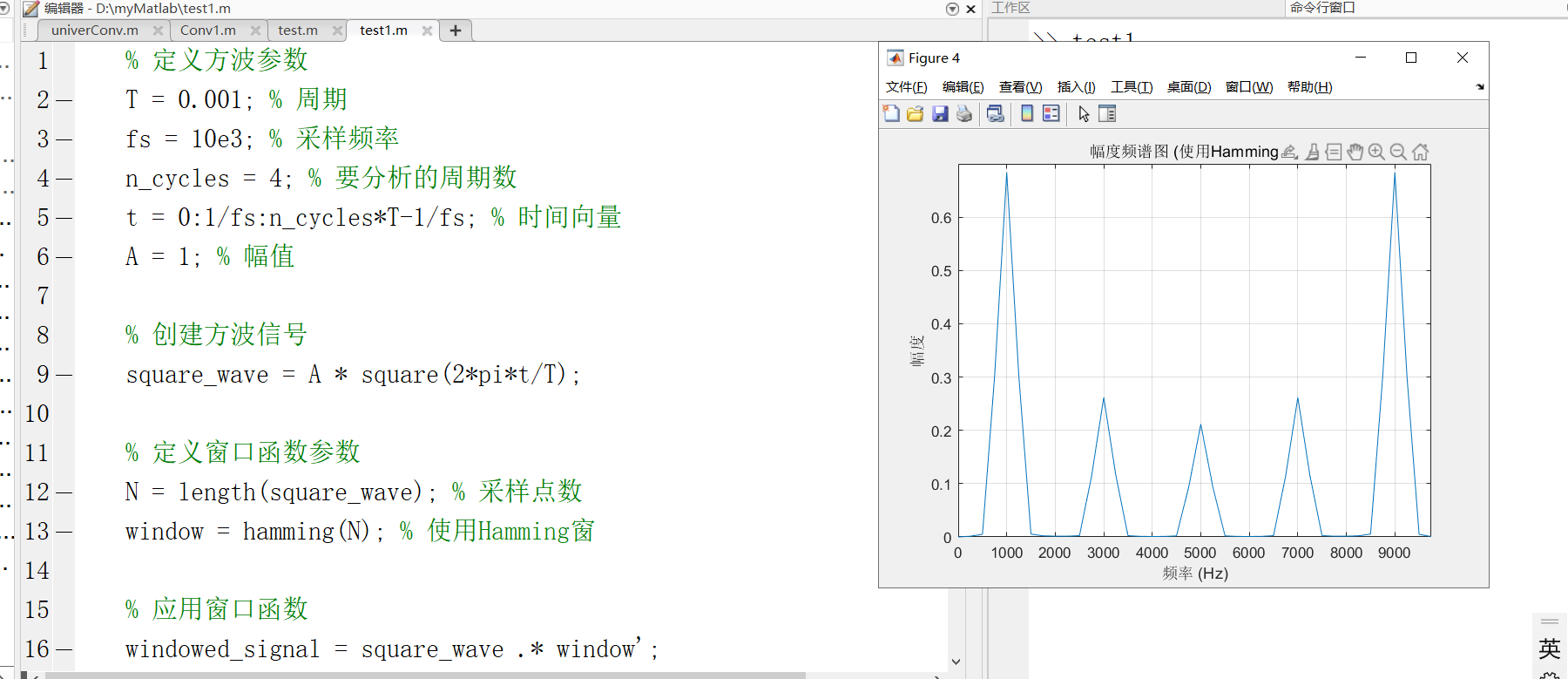
3）代码

% 定义方波参数  
T = 0.001; % 周期  
fs = 10e3; % 采样频率  
n_cycles = 4; % 要分析的周期数  
t = 0:1/fs:n_cycles*T-1/fs; % 时间向量  
A = 1; % 幅值  % 创建方波信号  
square_wave = A * square(2*pi*t/T);  % 定义窗口函数参数  
N = length(square_wave); % 采样点数  
window = hamming(N); % 使用Hamming窗  % 应用窗口函数  
windowed_signal = square_wave .* window';  % 计算DFT并获取幅度频谱  
X = fft(windowed_signal);  
amp1= abs(X)/N; % 归一化幅度  
amp1(2:end-1) = 2*amp1(2:end-1); % 对于实数信号，对称频率分量幅度加倍  
df=fs/N;  % 频率分辨率
f = (0:N-1)*df; % 频率向量  % 绘制幅度频谱图  
figure;  
plot(f, amp1);  
title('幅度频谱图 (使用Hamming窗)');  
xlabel('频率 (Hz)');  
ylabel('幅度');  
grid on;  
xlim([0 fs/2]); % 通常只绘制一半的频率范围，因为对于实信号，频谱是对称的

4，设计一个滤波器，滤除该信号中三次谐波及以上的频率成分，画出滤波器的频响特性曲线；

1）前期基础

①确定截止频率fc

要设计一个滤波器以滤除方波信号中三次谐波及以上的频率成分，可以使用MATLAB中的滤波器设计工具。对于方波信号，其频谱包含基频的奇数次谐波，因此我需要设计一个低通滤波器，其截止频率fc位于基频f0和三次谐波f3之间。

②步骤

首先截止频率位于基频f0和三次谐波f3之间的一个值。
接着，使用butter函数设计一个巴特沃斯低通滤波器，并指定了滤波器的阶数。
使用freqz函数计算滤波器的频率响应，并返回幅度和频率值。
最后，使用plot函数绘制滤波器的频响特性曲线，并标注截止频率和三次谐波频率的位置。

③注意点

滤波器的设计和性能会受到所选滤波器类型、阶数以及截止频率的影响。
在实际应用中，可能需要根据具体需求调整这些参数以达到最佳效果。
此外，巴特沃斯滤波器是一种常用的滤波器类型，但还有其他类型的滤波器可供选择，如切比雪夫滤波器或椭圆滤波器，它们可能在某些方面具有更好的性能。

2）频响特性曲线

3）代码

%信号的参数
T = 0.001; % 周期
f0 = 1/T; % 基频
f3 = 3*f0; % 三次谐波频率
fs = 10e3; % 采样频率% 设计低通滤波器，截止频率在基频和三次谐波之间
% 例如，我们可以选择截止频率为1.5倍基频
fc = 1.5*f0; % 截止频率
Wn = fc/(fs/2); % 归一化截止频率% 使用butter函数设计一个巴特沃斯低通滤波器
% 这里我们选择滤波器的阶数为4，可以根据需要调整
[b, a] = butter(4, Wn);% 计算滤波器的频率响应
[h, w] = freqz(b, a, 1024, fs);% 绘制滤波器的频响特性曲线
figure;
plot(w/pi, abs(h));
title('滤波器频响特性曲线');
xlabel('归一化频率 (x\pi rad/sample)');
ylabel('幅度/dB');
grid on;
axis([0 1 -100 1.1]); % 设置坐标轴范围以更好地显示曲线

5，用设计的滤波器对信号滤波，画出滤波器的输出信号的时域波形和幅度频谱图。

1）前期基础

要使用上面（4）中设计的滤波器对信号进行滤波，并绘制滤波后信号的时域波形和幅度频谱图，我需要先应用滤波器到原始信号上。

步骤

首先定义方波信号的参数，并创建了原始方波信号。
接着，按照之前的步骤设计了低通滤波器。
然后，使用filter函数将滤波器应用到原始信号上，得到滤波后的信号。
在绘制部分，使用subplot函数将时域波形和频谱图放在同一个图形窗口中。 1）首先绘制滤波后信号的时域波形， 2）然后计算滤波后信号的FFT并绘制其幅度频谱图。
因为FFT的结果是对称的，所以只绘制了正频率部分的频谱。

2）滤波后信号的时域波形和幅度频谱图

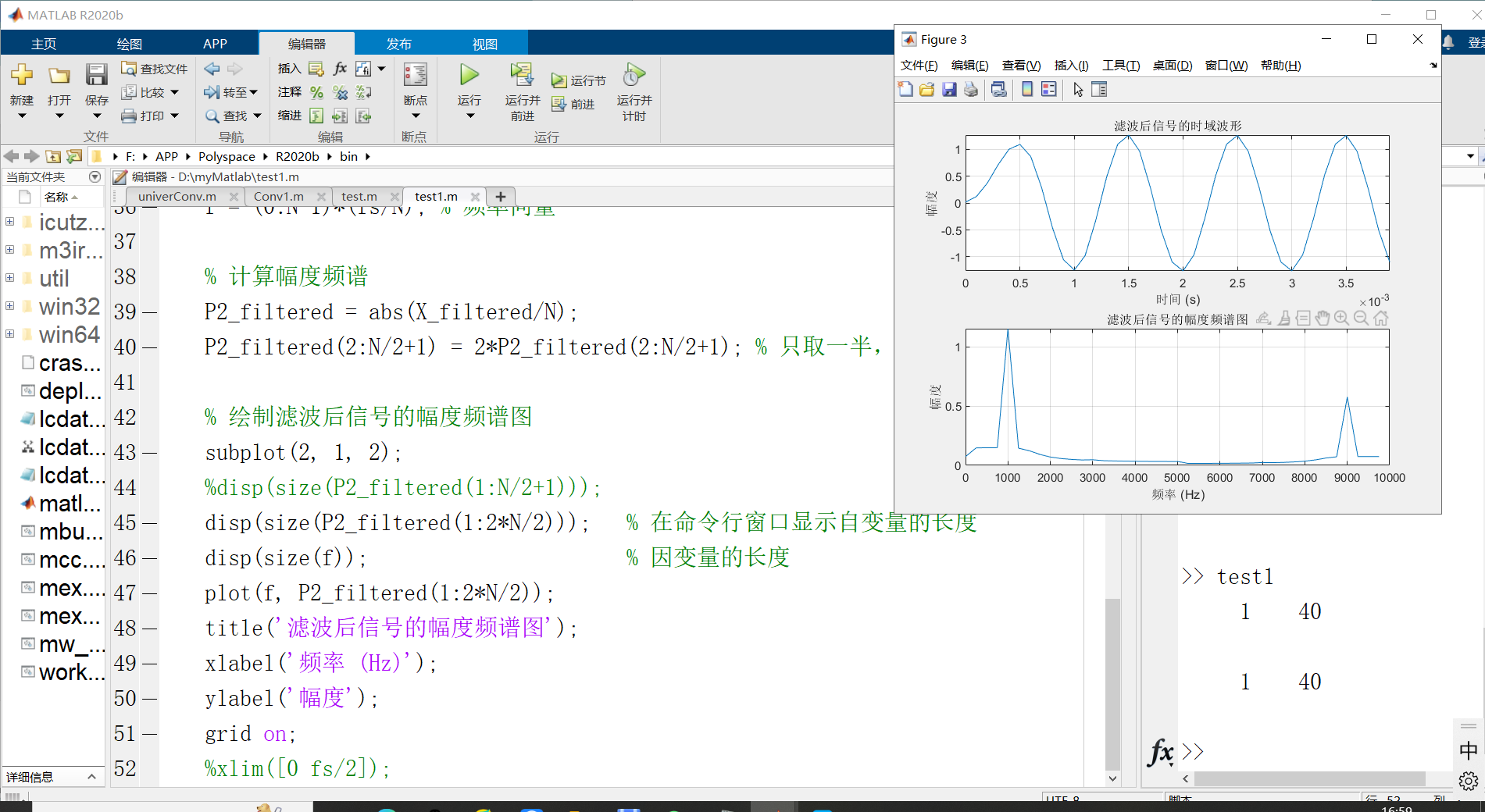
上面显示滤波后信号的时域波形，下面显示滤波后信号的幅度频谱图。通过比较滤波前后的信号，就可以看到滤波器成功地去除了三次谐波及以上的频率成分。

3）代码

% 定义方波参数  
T = 0.001; % 周期  
fs = 10e3; % 采样频率  
A = 1; % 幅值  
Ts=1/fs;  % 采样周期
num_cycles = 4; % 信号包含的周期数  
t = 0:Ts:(num_cycles*T)-Ts; % 时间向量  % 创建方波信号  
square_wave = A * square(2*pi*t/T);  % 设计低通滤波器  
f0 = 1/T; % 基频  
f3 = 3*f0; % 三次谐波频率  
fc = 1.5*f0; % 截止频率  
Wn = fc/(fs/2); % 归一化截止频率  
[b, a] = butter(4, Wn); % 设计巴特沃斯低通滤波器  % 应用滤波器到信号  
filtered_signal = filter(b, a, square_wave);  % 绘制滤波后信号的时域波形  
figure;  
subplot(2, 1, 1);  
plot(t, filtered_signal);  
title('滤波后信号的时域波形');  
xlabel('时间 (s)');  
ylabel('幅度');  
grid on;  
xlim([t(1) t(end)]);  
ylim([-A*1.1 A*1.1]);  % 计算滤波后信号的FFT并获取频谱  
N = length(filtered_signal); % 采样点数  
X_filtered = fft(filtered_signal); % 计算FFT  
f = (0:N-1)*(fs/N); % 频率向量  % 计算幅度频谱  
P2_filtered = abs(X_filtered/N);  
P2_filtered(2:N/2+1) = 2*P2_filtered(2:N/2+1); % 只取一半，因为是对称的  % 绘制滤波后信号的幅度频谱图  
subplot(2, 1, 2);  
%disp(size(P2_filtered(1:N/2+1)));
disp(size(P2_filtered(1:2*N/2)));   % 在命令行窗口显示自变量的长度
disp(size(f));                      % 因变量的长度
plot(f, P2_filtered(1:2*N/2));  
title('滤波后信号的幅度频谱图');  
xlabel('频率 (Hz)');  
ylabel('幅度');  
grid on;  
%xlim([0 fs/2]);

以上仅供参考，如果文章有错误的请在评论区指出，有疑问的也可以在评论区留言。1天8h在线。