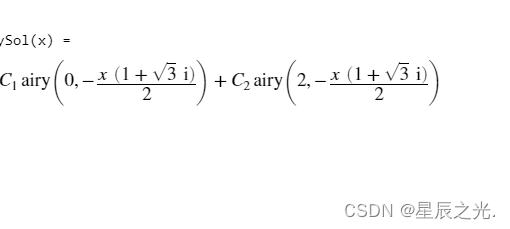工具/材料

matlab 2016a

打开matlab，首先定义变量x：

syms x;

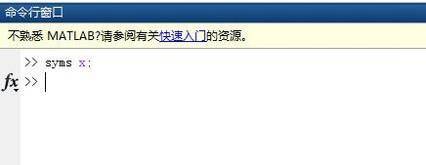
matlab中solve函数的格式是solve(f(x), x)，求解的是f(x) = 0的解。

第一个例子，求解最常见的一元二次方程x^2-3*x+1=0:

solve(x^2-3*x+1,x)，解出的结果用精确的根式表示。

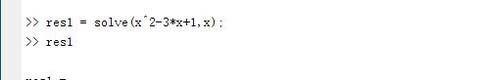
matlab解出的根不仅包含实根，也包含复根，例如求解三次方程x^3+1=0:

solve(x^3+1,x)

我们知道该方程有一对共轭复根，matlab也可以解出它的解。

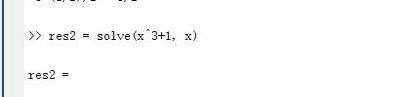
对于超出5次(含)以上的一元函数，有时无法用solve指令求的对应的根，如下图所示。这时可以使用roots命令求解。roots命令的参数是方程的各个系数按高次幂到低次幂排列成的向量，例如x^5+3*x^4-5*x^3+4*x^2-6*x+2=0，如果用solve指令得到的结果不能令人满意，而用roots就可以得到满意的结果。

对于非多项式方程，只能使用solve求解。例如求解exp(-x)-x^2+3=0的解如下。通过黄色的警告可以看出，这样的方程没有解析解，与我们已知的知识相同。

最后一类方程，是一元一次方程组。这是matlab最擅长的运算，可以使用矩阵进行求解。对于齐次线性方程来讲，使用null(A,'r')。其中'r'表示使用简化阶梯型行列式求解。对于如下的方程，可以解得线性无关的一组解。这样，我们还可以引入常量k1与k2表达通解。

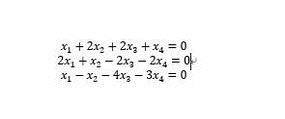
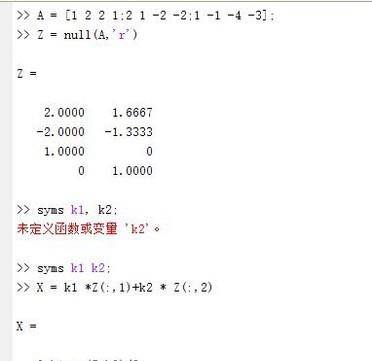
对于线性非齐次的解，可以使用linsolve(A,b)。其中A是系数矩阵，b是非齐次项(如果b是多列矩阵，意味着解多个砼系数不同齐次项的方程组)。对于图中的方程组，可已这样求解。

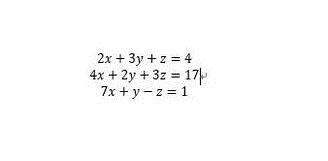
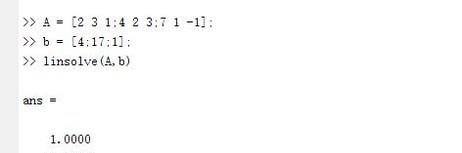
特别提示

matlab求解方程的方法有很多，要找到适合自己需要的方法，需要多加练习。