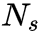《An Ideal-Security Protocol for Order-Preserving Encoding》论文学习笔记

OPE（保序加密）：密文的排序顺序与对应的明文的排序顺序相匹配的加密方案。
论文中提出的保序加密的理想安全保证是密文除顺序外不透露任何与明文有关的信息。

1.论文背景

加密是一种强大的技术，可以保护存储在不可信服务器（如云计算）上数据。 但是其中一个限制是，通常应用程序必须对数据进行解密，以便对数据进行处理。例如，查询加密的数据库或对加密的电子邮件消息进行排序，这些都需要一个信任的服务器来运行该应用程序。 对加密数据进行计算的方法避免了由未知不可信的服务器对数据进行解密的需要。 虽然最近关于全同态加密的一些工作表明，原则上可以对加密数据执行任意计算，但其带来的性能开销高得令人望而却步，大约是10⁹倍。

鉴于此，我们可以允许不受信任的服务器对密文进行计算操作，其中一个常见的操作是顺序比较，用于排序、范围检查、排序等。为了允许不受信任的服务器对密文执行顺序比较，研究领域和工业场景中的许多系统都使用order-preserving encryption or encoding方案，即当 x > y时有 Enc(x) > Enc(y) 的方案。将这种方案缩写为OPE。

OPE 主要在数据库中用于处理对加密数据的 SQL 查询 ，同时也应用于各个web应用程序和软件等。数据库服务器可以构建索引、执行SQL范围查询和对加密数据进行排序，所有这些操作都与对明文数据的操作相同。这个特性也具有良好的性能，并且只需对现有软件进行最小的更改，从而使其易于采用。

当前的 OPE 方案都不能完全防止攻击者窃取机密数据的隐私，而不仅仅是了解密文的顺序。本文提出了第一种理想安全的保序编码方案，其中密文只揭示明文值的顺序，除此之外什么也不泄露。在这种方案中，加密协议是交互式的，并且当新的明文值被加密时，为了保持密文顺序的正确性，已经被加密的值的少量密文是可以改变的。我们称这种方案为mutable order-preserving encoding，即mOPE，为了强调，密文的可变性，此处作者使用encoding来替换encryption。

2.论文概述

mOPE 的工作原理是构建一个平衡的搜索树，其中包含应用程序所有明文值被加密后的密文值。关键值的保序编码是搜索树中从树根到该值的路径。例如，如果 x 小于 y，则到 x 的路径将在到 y 的路径的左侧；我们使用二进制编码表示树路径，其中编码在树中从左到右递增。搜索树和加密数据一样都存储在不受信任的服务器上，可信客户端通过使用交互式协议将加密的值插入到树中。路径编码的长度就等于树的深度，因此为了确保密文不会变得任意长，mOPE会重新平衡搜索树。这需要更新密文对应的数据项的位置在树中的改变。实验表明，只有少量的已经加密的值会改变密文的每个新编码的值。

在前人工作基础上的最强安全定义是由Boldyreva等人提出的IND-OCPA。IND-OCPA为保序方案提供了理想的安全性：可以访问一组密文的攻击者不能获知关于其明文值的任何信息，除了它们的顺序。而现有方案均未达到IND-OCPA，本文的结构mOPE是第一个实现IND-OCPA的。

在本文中，作者还提出了一个新的安全定义，称为same-time OPE security，这要求对手只能获知同时存储在应用程序中的数据项的顺序，其余一无所知。这个定义比IND-OCPA强，我们展示了mOPE的扩展如何实现这个更强的定义。

3.威胁模型

论文中的模型由一个OPE客户端和一个OPE服务器相互交互。客户端是要加密的数据的所有者，因此客户端是可信的。OPE服务器不受信任。我们考虑以下两个关于服务器的威胁模型：
①被动的（或诚实但好奇的）的敌手：服务器正确地遵循我们的协议，并向OPE客户端返回正确的答案，但它试图学习有关数据的除了顺序之外的其他信息。例如，服务器可以记录操作和数据的整个历史版本，将数据提供给某个其他方，甚至使用一些辅助信息来尝试了解更多关于数据的信息。②主动的(或恶意的)对手：服务器可以以任何方式不诚实，比如给客户端返回不正确的答案。

4.mOPE的原理

☆Tree construction

使编码后的值在服务器上组成一个平衡二叉搜索树。对于每个节点v, v的左子树中的所有节点都严格小于v，而v的右子树中的所有节点都严格大于v。在这里使用的是B-Tree，关于B-Tree的原理，可以参照之前的博客。

选择B树是因为它对于mOPE有很多优点：它对插入、删除和查找的最坏情况代价也只是对数级别的，它支持高效的密文更新，并且它便于验证恶意服务器产生的答案是否正确。

在mOPE的树中，树的每个节点都包含一个值的DET加密(在客户端的秘钥sk下加密)，但密文是根据明文值的顺序排列在树中的。OPE Tree的结构如下：

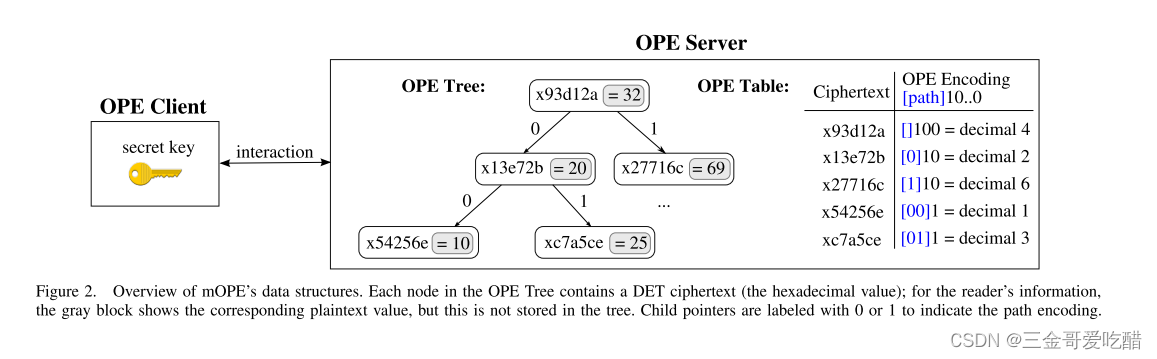
由于客户端可能会加密大量的值，所以我们将此树存储在不受信任的服务器上。我们可以看到，每个节点左子树的明文值都小于该节点的值，而右子树的明文值都大于该节点的值。

当然，服务器不知道底层的明文值，所以它不能以这种形式排列树。而客户端将帮助服务器在树中找到插入值的位置。

那么客户端是如何做到的呢？举个例子，假设客户端想要使用图2中所示的树来对55进行编码。客户端首先请求树的根节点，服务器返回x93d12a，客户端将其解密为32。由于55>32，客户端向服务器请求根的右子节点，服务器以x27716c响应，客户端将其解密为69。然后，客户端请求69这个节点的左子节点，服务器响应目前没有这样的子节点。这意味着客户端可以在这个位置插入一个新节点，也就是DET加密后的值。

注意，客户端对服务器泄露的只有顺序信息(例如根据编码的值可以判断一个值在另一个值的左边或者是右边)，因此这种交互没有透露其他除了顺序意外的任何信息。

以下是关于对一个值v进行OPE的遍历：

①首先，客户端会向服务器请求OPE树根位置上的密文c’；
②客户端解密c’并获得解密后的明文v’；
③如果v < v '，客户端告诉服务器" left “;如果v = v '客户端告诉服务器” found ";如果v > v '，客户端告诉服务器“right”。
④服务器根据客户机的信息返回下一个密文c”，并返回到步骤2；
⑤当找到v，或者当服务器到达树中的空节点时，算法停止。

算法返回的结果是OPE树中的结果指针、从根开始的OPE树的路径以及是否找到了v。

☆Binary encoding

那么新插入值55的OPE编码是多少呢？从根到节点的路径表明了该节点相对于其他树节点的相对顺序。用“0”位标记每条左边，用“1”位标记每条右边，然后就可以用相应树边的按位拼接来表示从根结点到节点的路径。例如，在图1中，10的路径是(二进制)00，转化成十进制就是0；25的路径是(二进制)01，转换成十进制就是1;55的路径是(二进制)10，也就是十进制的2。其对应的十进制也就揭示了它们对应的明文顺序的信息。

此处注意对于树中较高的节点：例如，树根32的路径编码是空字符串，既不大于0且小于2。因此，我们将所有路径填充到相同长度，对于值的OPE编码定义如下：
$$OPEencoding=[path]\mathrm{10...0},$$
将每个值填充到与期望的密文大小m所需的一样多的比特位。例如，图2中m= 3，则根值32的编码是十进制4（顺序），10的编码是十进制1，并且55的编码是十进制5。我们可以看到，所有值的编码顺序都保留为和明文一样。

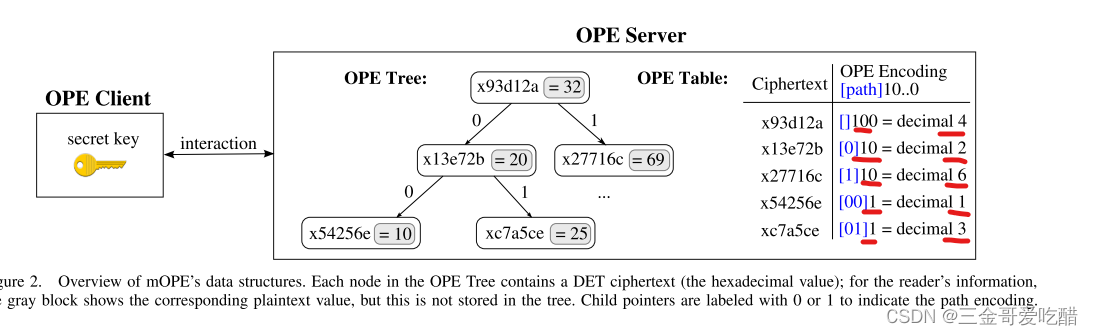
☆Tree balancing

如果主键是顺序插入的，则会形成一个单向链表，查询性能大大降低。在数据量很大的情况下，层级较深，检索速度就慢（红黑树也会面临这样的问题）。所以mOPE需将树保持在对数高度。例如B-Tree就有这样的性质。

而树的平衡正是使OPE编码改变的原因，因为在重新平衡之后，节点可以移动到树的不同位置，从而使其在树中的路径发生改变。这也就是mOPE相对于OPE作出改进的地方，因为原始的OPE编码方案具有非常长的OPE编码。

在平衡了OPE树之后，OPE服务器必须更新所有包含OPE编码的服务器端存储的数据(例如，更新数据库中的相关值)。所以将OPE服务器与OPE方案的系统放在一起是非常重要的。

☆平均开销

客户端是O(logn)，其中n是编码的值的总数，保持顺序的编码只需要O(log n)位，这是因为树的高度是对数级别的。此外，客户端不需要参与再平衡：即使服务器不知道底层的明文值，服务器也可以在不需要任何客户端参与的情况下使树再平衡，因为它只需要知道顺序信息，这些信息已经可以从服务器自己存储的树中获得。

☆旧的编码

树的再平衡带来了另一个挑战，因为特定值的OPE编码可能会过时。应用程序首先通过调用OPE客户端获得某个值的OPE编码，然后执行更多的工作，但重新平衡树的操作可能导致应用程序的原始OPE编码变得陈旧，这意味着编码不再对应于值在树中的位置。如果应用程序使用陈旧的编码，可能会获得不正确的结果。

为了防止出现这样的情况，在服务器上引入了一个名为OPE Table的映射，如图2所示。每当在树中插入一个新记录，或者服务器重新平衡树时，就更新OPE表，将DET密文映射到它们新的或更新的OPE编码上。使用这个OPE Table，客户端只需要跟踪永不过期的DET密文，就可以放心地执行他想要的操作。对于一个DET密文，服务器可以在任何时候计算OPE编码，而不需要客户端的帮助。因此，我们设想OPE编码将只存储在服务器内部，可以根据需要重写。另外，OPE Table还可以用作缓存，在编码重复值时保存客户端工作进度。

下面介绍具体的mOPE方案。

☆Mutable order-preserving encoding (mOPE)

用于明文域D的可变保序加密方案是由客户端和有状态服务器运行的多项式时间算法mOPE=（KeyGen，InitState，Enc，Dec，Order）的元组，其中KeyGen是概率性的，其余是确定性的，并且Enc是交互式的。下面介绍一些算法：

· Key generation: sk ← KeyGen(1^κ)：KeyGen在客户端运行，将安全参数k作为输入，并且输出密钥sk。

· Initializing server state: st ← InitState(1^κ)：InitState作为服务器运行，将安全参数κ作为输入，并输出初始状态st。

· Encryption: (c, st′) ←Enc(sk,v, st)：Enc是客户机和服务器之间的一种交互式算法。客户端输入sk和v，服务器端输入状态st。最后，客户端得到密文c，服务器端得到新的状态st '。Enc的运行时间是|sk|和|v|的一个固定多项式。

· Decryption: v←Dec(sk,c)：客户端通过输入私钥sk和密文c，执行Dec，得到明文v。

· Ordering: e ← Order(st,c)：Order在服务器上运行，以状态st和密文c作为输入，并输出保留顺序的编码e。

在实际应用中，e的值很少会随着st而改变（因为树中给定的节点很少会被重新平衡）。可以将e的值存储在磁盘上，当树需要平衡时再更新它。这样客户端不会担心编码会过时，所以这种mOPE算法的方案如下：

a. 密钥生成：客户端执行
b. 初始化服务器：即初始化OPE Tree和 OPE Table（仅包含±∞），返回一个初始状态的st（代表服务器的状态）
c. 加密（插入）：
客户端：将明文v进行加密（加密算法可以是任意的算法， eg：AES），密文为c，并将c 发送到服务器端
服务器端：
①查询是否c在OPE Tree中，如果在则返回没有改变的st，否则在OPE Tree中插入在c，并计算c的OPE encoding，更新OPE Table
② 如果OPE Tree需要去平衡，平衡OPE Tree，并更新所有的受影响的节点的OPE encoding。
③ 服务器返回一个新的状态st，
d. 解密：在客户端执行，将c解密为v
e. 查找排序：如果c在OPE Table 中，将OPE Table相应的编码返回，否则返回error

面对威胁1，使用的是stOPE，其方案如下：

a. 初始化：（Initialization）: 客户端生成一个密钥，而服务器也初始化它的状态。
b. 插入（Insert）:（RND代表对称加密）
客户端: 计算c ← RND.Enc(sk, v)，并将c发送到服务器
服务器：遍历OPE Tree，如果存在c，说明已经c之前被加过了，计算相应的OPE编码e。如果对于v的密文c_t 存在，服务器增加它的ref-count（表示这个值被插入的次数），如果v已经不在这个OPE Tree中，将c插入到OPE Tree并且ref-count=1。
c. 删除（Remove）：
客户端: 计算c ← RND.Enc(sk, v) ，并将c发送到服务器.
服务器：遍历OPE Tree，
如果c不存在，返回error；
如果c存在且ref-count >1, 则ref-count = ref-count -1；
如果c存在且ref-count =1，将c从OPE Tree和OPE Table中移除；
如果节点删除触发树平衡，服务器也会类似地更新OPE Table和任何包含那些OPE Encoding的存储器。
d. 查询（Query）: 查找到最贴近v的v_1,v_2，使得v_1≤v< v_2
客户端: 计算c ← RND.Enc(sk, v) ，并将c发送到服务器.
服务器：遍历OPE Tree，按照性质3来定位最邻近的间隔。
查找排序：如果c在OPE Table 中，将OPE Table相应的编码返回，否则返回error

这里注意，不能使用DET进行加密，因为DET会暴露一个新值是否等于先前删除的值，这就暴露了除了顺序以外其他的信息。因此,OPE树中的密文使用的是RND。

面对威胁2：恶意的服务器可能会改变它对客户端的响应，试图在加密值的顺序上了解更多的信息。例如，我们如果删除一个值之后再插入新的值，它可能不会从OPE树中删除旧的值，这将泄露旧值的顺序，从而违反同一时间的OPE安全性。那么为了强制服务器正确地执行这些操作，我们在OPE Tree上添加Merkle哈希，并使用它检查服务器响应的正确性。

带有默克尔树的OPE树的哈希值如下：

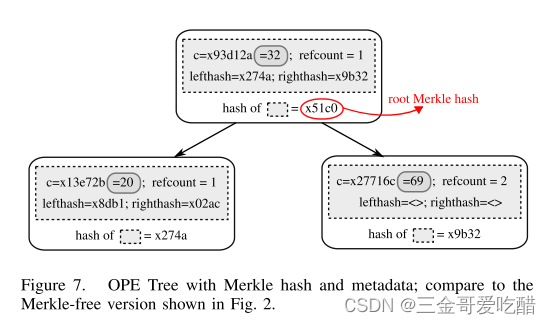
为了验证服务器执行的每个操作的正确性，客户端存储一个Merkle树根哈希值的副本，并为每个操作向服务器请求证明。例如，为了让客户端检查节点v是否在OPE树中，服务器必须提供一个sibling-path：这包括在从V到树根节点的路径的所有信息（包括哈希值），以及在这些节点的所有兄弟节点处的信息。使用Merkle树的属性，为了确定v在树中，客户机只需计算对应于兄弟路径的Merkle根，并查看它是否与客户机存储的哈希值相匹配。

当客户端请求插入或删除一个数据项时，服务器需要提供它确实插入或删除该数据项的证明。证明由以下部分组成：

1）旧的Merkle信息：树中关于插入/删除影响的节点的信息，以及这些节点的兄弟节点的路径。
2）新的Merkle信息：新的sibling-path与删除该节点后，被插入的新的节点的值和哈希值。

客户端通过以下方式检查插入或删除证据：

1）使用旧的Merkle信息，客户端计算Merkle树的根，并验证它与客户端具有的当前Merkle根一致。
2）客户端检查新信息是否正确：节点在B树中被正确地插入或移除，或者适当的引用计数被更新，并且节点处的任何其它元数据不被改变。
3）客户端计算新树的根并存储更新后的Merkle哈希。