数学上经常需要解方程。现在有函数: f(x) = 2x^5+7x^3+100,求f(x)=y解。
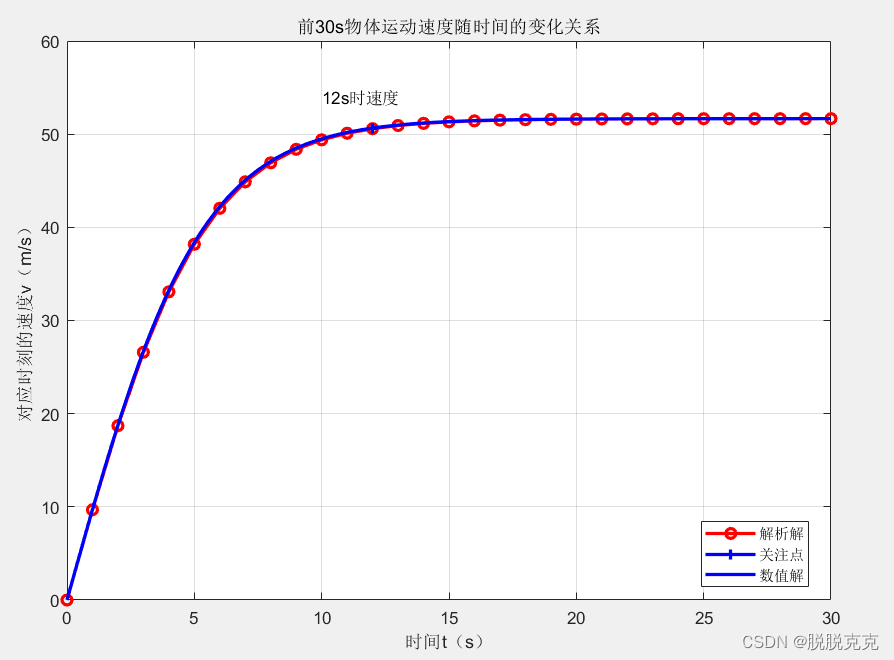
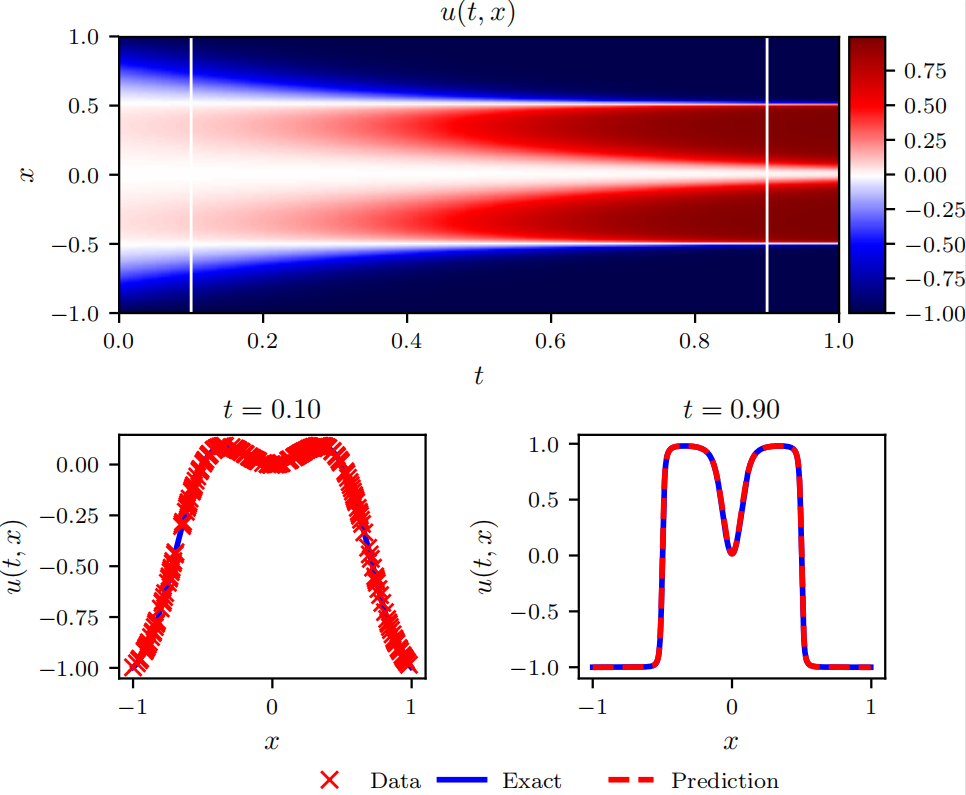
提示:下面是goc程序画出的函数图形,可以看出函数是单调上升的。
输入格式
第一行1个实数:y,范围在[-1000000000,1000000000]。
输出格式
一个实数x,使得f(x)=y。
x的精度小于0.001。
输入/输出例子1
输入:
200
输出:
1.91184
//Find()函数,用二分法////首先大致 判断x的取值范围, 从y的最值来判断// x的取值范围【-200.0,200.0】//#include <bits/stdc++.h>using namespace std;const double maxX = 200.0;const double minX = -200.0;const double eps = 0.000001;double Y;double Cal(double X){// return 3*X+7;// return 3*(X*X)+7; double res = 2*(X*X*X*X*X) + 7*(X*X*X) + 100;return res;}double FindKey(double Y){ //查找Y对应的X值,二分法if(abs(Cal(minX)-Y) < eps) return minX;if(abs(Cal(minX)-Y) < eps) return maxX;double L = minX, R = maxX;while(L + eps < R){double mid = L + (R-L)/2;if(Cal(mid) <= Y) L = mid;else R = mid;//cout<<"L="<<L<<" ";//cout<<"R="<<R<<endl;}return L;}int main(){cin>>Y;//cout<<Cal(2500)<<endl;cout<<FindKey(Y)<<endl;return 0;}/** 这是解整数方程的例子* 函数为:y=3x+7; y=3x^2+7; y=3x^3+2x^2+7 (选一个就可以了)** y的取值:范围在[-1000000000,1000000000]。** 输入: y值 13, 10, 12 * 输出: x值 2,1,1** * *///Find()函数,用二分法////首先大致 判断x的取值范围, 从y的最值来判断// y=3x+7; x的取值跟y值一样[-1000000000,1000000000]。// y=3x^2+7; x的取值范围【-10000, 10000】// y=3x^3+2x^2+7 ; x的取值范围【-1000,1000】//#include <bits/stdc++.h>using namespace std;//y=3x+7; //const int maxX = 1000000000;//const int minX = -1000000000;// y=3x^2+7; //const int maxX = 10000;//const int minX = -10000;// y=3x^3+2x^2+7 ;const int maxX = 1000;const int minX = -1000;int Y;long long Cal(int X){// return 3*X+7;// return 3*(X*X)+7; long long res = 3*(X*X*X)+2*(X*X)+7; return res;}int FindKey(long long Y){ //查找Y对应的X值,二分法if(Cal(minX) == Y) return minX;if(Cal(maxX) == Y) return maxX;int L = minX, R = maxX;while(L+1 < R){ int mid = L + (R-L)/2;if(Cal(mid) <= Y) L = mid;else R = mid;cout<<"L="<<L<<" ";cout<<"R="<<R<<endl;}return L;}int main(){ cin>>Y;//cout<<Cal(2500)<<endl;cout<<FindKey(Y)<<endl;return 0;}