点击蓝色“有关SQL”关注我哟
加个“星标”,天天与10000人一起快乐成长
这两本书,分别是:
《Spark 快速大数据分析》 (英文书名《Learning Spark: Lightning-fast Data Analysis》)
《Spark高级数据分析》影印版(英文书名《Advanced Analytics with Spark》)
我第一时间在朋友圈分享这两本时,很多朋友都跑来“指点”我,你怎么可以看这两本书呢,你应该看 xxx, xxx.
读书是件很私密的事情,别人告诉你怎么怎么滴,没有卵用。
你的理解力,你的背景知识结构,没有人比你更清楚。什么阶段看什么样的书,什么样的书,适合自己读,需要自己去体验。
别人给你的书单,往往比较“他化”,带着“他”或“她”的读书品味。如果书单系统化还行,我最怕的是,在别人的口里做人,做事。万一错过自己应该学到的,能找上门去算账么?或许有些人会,但我肯定羞于这么干。
首先来看第一本《Spark快速大数据分析》。这本书的4位原作者,清一色技术出身,全是 Databricks 创始人。而 Databricks 正是孵化 Apache Spark 的公司。
全书210页,非常薄。我知道大家都深恶痛绝大砖头,包括学霸都是。
记得余晟老师(沪江网CTO)曾经在一次访谈中谈及翻译正则表达式那本经典书。也是大部头,他怎么做的呢?趁心血来潮,把书的前半部分翻译个上百页,实在无聊了,再从中间挑个上百页来翻。来回翻腾几次,书也就翻完了。
所以用这本200页的书来做入门,非常适宜。
如果你是位新手,对分布式计算很陌生,只是偶尔从我们微信公众号《有关SQL》听到过这么一个概念,但你有些编程经验,对多线程,多进程也稍稍耳熟。那么本书的第一部分,5个章节,不到90页书,绝对可以让你快速熟络 Spark.
Spark 总体框架,可以理解是多线程,多进程的衍生。将任务切割,分发到很多计算机上处理。我大学同学,老胡,跟我分享过一个很有意思的例子。你听听看。
有天植物生理课,我们在花房修剪残枝,老读者都知道,我是学农学的嘛。他指着根木柴问我,如何让这根木柴烧得更快?
听到这样的开放题,我就很开心,当然是浇上汽油。
他似乎没有被我的笑话冷到,自问自答,把木柴尽可能对半砍,两头点上火。砍的次数越多,烧得越快。
虽然在植物课上提出这样的题,有些奇怪,但更奇怪的是,后来每次用多线程编程,我总想到这个例子。
Spark 原理也一样。一台计算机的计算资源(CPU个数)总是恒定的,当多线程沾满资源时,加快计算的唯一方案,就是利用多台机器。
多线程会有一个主程控制整个过程,Spark 也有这样一个主程,控制每台计算机上跑的进程,这个主程,就是 Driver 程序。切割到每台机器上的计算任务,就由 RDD 包装起来。
短短这90页,可以充分学到 Spark 的核心编程知识。极力推荐各位好好看。多读几遍,除非你脑回路惊奇,不然书读百遍,才是yyds.
纵观全书,我认为可以分成 3 部分。
上面我冒死推荐的,是第一部分。接下来两部分,是进阶篇和实用篇。想要做点实事,必须要会。
第六章到第八章,是编程进阶。如果说前五章,让初学者可以快速操作数据,那么这三章,就可以拿来实战。比如维度表的 Join, Spark 应用的提交以及并行化处理的优化,等等。
第九章开始到11章结束,讲的是 Spark 技术栈的应用。比如 Spark SQL, Spark Streaming 和 Spark 机器学习。这三章都偏场景应用,可以快速浏览。想要深入,请搭配其他书一起看。比如对于 Spark 机器学习,下面提到的第二本书,就是绝佳伴侣。
机器学习本身是非常广的一个领域,Spark 对它来说,不过是工具。在第一本书中,寥寥几页纸,真是不够的。所以我挑了第二本书来看。这本绝对彪高你的求知荷尔蒙!
来看下书的目录:

都是和机器学习相关的场景应用。这种学起来才带劲。
大数据就一工具,如果一开始就蒙头钻研其内部,被她魅惑了很长时间,这样不仅没有发挥她最大的功效,而且还会打击你的积极性。
就像车,造出来是为了让你开的。只有在开的过程中,你才有可能发现,燃油转换率不高,刹车灵敏度不够,车身最高平稳驾驶速度,等等问题。恰巧你是改装车迷,那么神仙也挡不住你动手了。
如果你是新手,小白,拿到一台车,不去驾驶,反而在研究各个零部件是怎么造的,请问,什么时候你才能带上妹子去兜风?
看这样的书,挑战不亚于每月跑10次10公里。刚开始极容易放弃,因为天气,因为加班。只有坚持过最难的那段坚持,才会被多巴胺给彻底征服。身心经历过汗水的洗礼,才会升华。
要做出真实的例子,看一本书完全不够。比如推荐算法 Alternating Least Squares Recommender :

为了看懂这里面的原理,设计和检测标准。我接连又去看了其他几本书,还有几篇论文。本书纯碎当做是按图索骥的地图,经过微信读书,甚至是 wikipedia 的检索阅读,最终才对推荐算法的的实验设计,步骤和评测标准有了些掌握。
本书在讲解 Alternating Least Squares Recommander 算法时,采用了 Latent-factor 模型。如果照着书中所讲述的学下去,可能知道的仅仅是推荐算法中的九牛一毛。真正业界研究火热的,是基于邻域的算法(neighborhood-based).
看到这里,我对推荐算法的实验设计产生了兴趣。一个标准的推荐引擎开发,到底要经历哪些步骤?有没有什么套路?
于是又找来一本囤积了好久的《推荐系统实践》(就是项亮那本,国内最早讲推荐系统)来看。
不得不说,这本书,才是推荐系统的入门经典。阅读了其中30页关于推荐系统的设计,渐渐对 《Advanced Analytics with Spark》有了更全面的认识。
比如,推荐系统乃至机器学习整个流程大致是这样的:
挑选数据模型
设计算法
挑选数据集
评测算法优劣
项亮这本书,系统化讲解了推荐算法的实践路线。罗列了很多数据模型,以及匹配的算法,还有这些算法之间的对比,性能如何。
经过一番检索,我才能知道,原来 Latent-factor 仅仅是一种算法,比他优秀的算法还有很多,各自用在哪些领域。在我头脑中,慢慢建立起一个完整的推荐算法地图。
当然,项亮的《推荐》也有门槛, 并不是所有对推荐一无所知的人,都可以快速掌握。比如像我这样,数学稀烂的人,对其中的很多术语,都需要喝上一杯星巴克,才能领悟的了。
在讲解精度(Precision)和召回率(Recall)时,项亮用了这两个公式和描述:

召回率描述有多少比例的用户—物品评分记录包含在最终的推荐列表中,而准确率描述最终的推荐列表中有多少比例是发生过的用户—物品评分记录
基于他的文字描述,我无法理解两者的概念。准备来说,是无法知道两者的真正不同。(看图中的公式和表述,一般读者估计也难懂)
于是,我又找了深度学习的花书。通过微信读书,看到花书中对精度和召回率的描述。依旧难解。
花书中,对Precision和Recall是这样描述的:

看完,我更晕了。怎么办,外事不决,问Google. 我默默打开了 wikipedia.
找到了这段解释:
Suppose a computer program for recognizing dogs (the relevant element) in photographs identifies eight dogs in a picture containing ten cats and twelve dogs, and of the eight it identifies as dogs, five actually are dogs (true positives), while the other three are cats (false positives). Seven dogs were missed (false negatives), and seven cats were correctly excluded (true negatives). The program's precision is then 5/8 (true positives / all positives) while its recall is 5/12 (true positives / relevant elements).
加上他的配图:

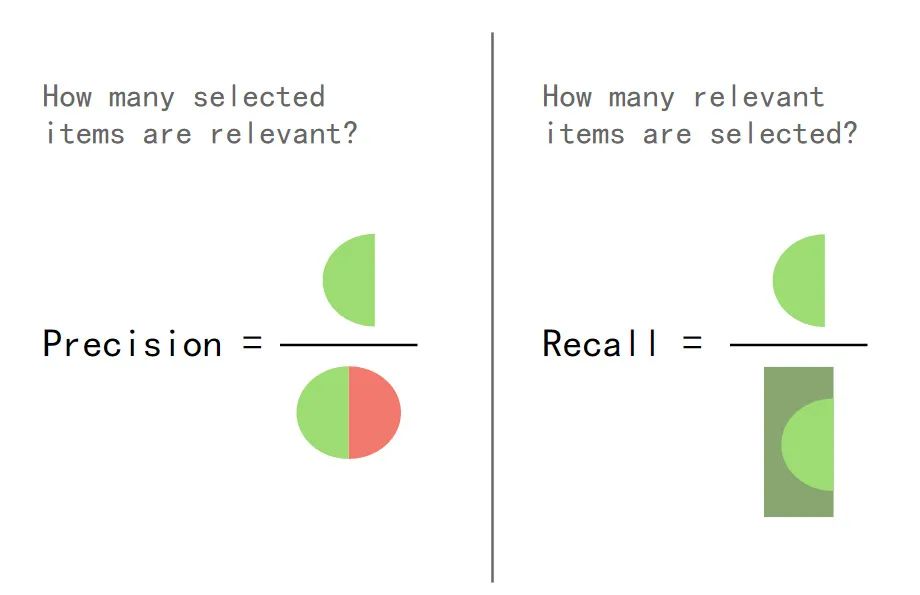
恍然大悟,这不就是我要的答案嘛!
在编程领域,“放弃实战,则开卷无益”,永远正确。通过实战领悟的技术才有意义,从而激发你更多的灵感。想想看,要是从统计学,具体数学和机器学习一路看上来,得花多少时间,去学一堆暂时用不了的知识,这完全违背实战主义的规律。
所以,在工作之后,我学会的一个技能,凡事先从“把大象装冰箱,需要几个步骤”开始构思。每一步再拆分可执行的小步骤,一步步攻克。
当然,如果你还在上大学,有大把时间,还是非常建议,努力提高自己的数学修养。你看,数学稀烂的我,只能被 CRUD 的巨浪淹没。
我的想法是5月份能把这本书看完,但事实上我真高估自己的水平了,这样的知识密度,一个月真不够读懂全书。
很多朋友会说,第一本书是2015年出版的,太老了,不适合看。那推荐买第二版的,全进口,600多RMB,我料他一定会说浪费钱。
当然我必须承认,第一本书以 Spark1.0 为基础讲的,与当前的版本说,是陈旧了不少。但基础知识还是没变,仍旧具有可读性。而且概念性写得比其他国内作者好太多。毕竟 Spark 火过那么一段时间,大量靠翻译文档出的书,国内有很多,但大多缺乏灵魂。
有些朋友,苹果设备,潮牌服装买得飞起,要他买本100块的书,恨不得马上能赚回10倍,才甘心。要不然一句费钱就完事。能花个几小时找盗版电子书,坚决不买正版书。不要这样。
对于我,买书是种乐趣;朋友圈打卡读书,也是;写书评,更是乐事一件。
--完--
往期精彩:
本号精华合集(三)
外企一道 SQL 面试题,刷掉 494 名候选人
我在面试数据库工程师候选人时,常问的一些题
零基础 SQL 数据库小白,从入门到精通的学习路线与书单