因2020年度业绩大幅预亏以及拟股权投资减值准备等，深交所于2月2日对向宋城演艺（SZ:300144）下发关注函，要求该公司进行补充说明。

据了解，今年1月30日，宋城演艺披露的《2020年度业绩预告》、《关于拟计提长期股权投资减值准备的提示性公告》显示，预计其2020年度的营业收入在8亿元至10亿元之间，而2019年为26.12亿元。

 

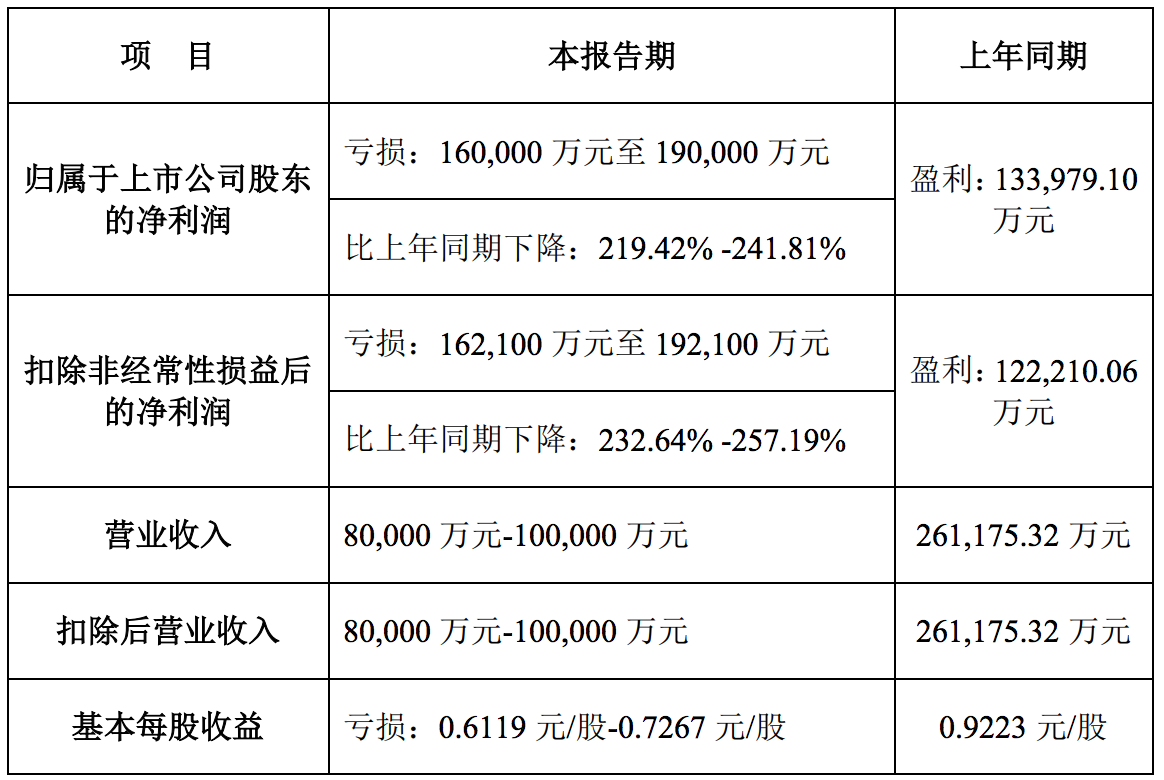
宋城演艺预计其2020年度亏损16亿元至19亿元，同比下降219.42%至241.81%，2019年同期为盈利13.40亿元；扣非净亏损16.21亿元至19.21亿元，同比下滑232.64%至257.19%，2019年同期为扣非后盈利12.22亿元。

宋城演艺称，业绩下降与疫情相关，其旗下各景区上半年几乎都处于闭园状态，2020年6月12日才重新营业。在市场环境不利的影响下，其演艺主业预计仍实现净利润约1.1亿元。

预告期内，重组后的数字娱乐平台花房科技总体业务发展良好，充值用户、消费用户及营业收入、经营性利润增长。分部看，花椒平台业绩增长，但六间房平台业绩下滑。

 

宋城演艺在公告中表示，拟对其持股37.06%的北京花房科技有限公司（下称“花房科技”，系以北京密境和风科技有限公司（下称“密境和风”，花椒直播运营主体）为会计主体）计提了资产减值。

受此影响，宋城演艺按权益法确认长期股权投资损失约7.24亿元。同时，宋城演艺对花房科技长期股权投资进行了减值测试，计提长期股权投资减值准备约11.08亿元，长期股权投资损失和减值准备合计约18.32亿元。

对此，深交所要求宋城演艺对比重组完成前后花房科技、密境和风的收入、成本、费用等与2019年度重组时盈利预测的差异，补充说明本次长期股权投资减值测试的详细过程。

同时，说明对花房科技股东全部权益价值（不含长期股权投资-密境和风股东全部权益价值）预测指标中，2021年至2025年预测营业收入不变的原因及合理性等。

贝多财经了解到，宋城演艺曾于2015年以26亿元的价格收购六间房。根据宋城演艺此前公告，2015年至2018年，六间房超额完成了业绩承诺，4年期间实现了净利润10.85亿元，超过承诺的9.94亿元。

 

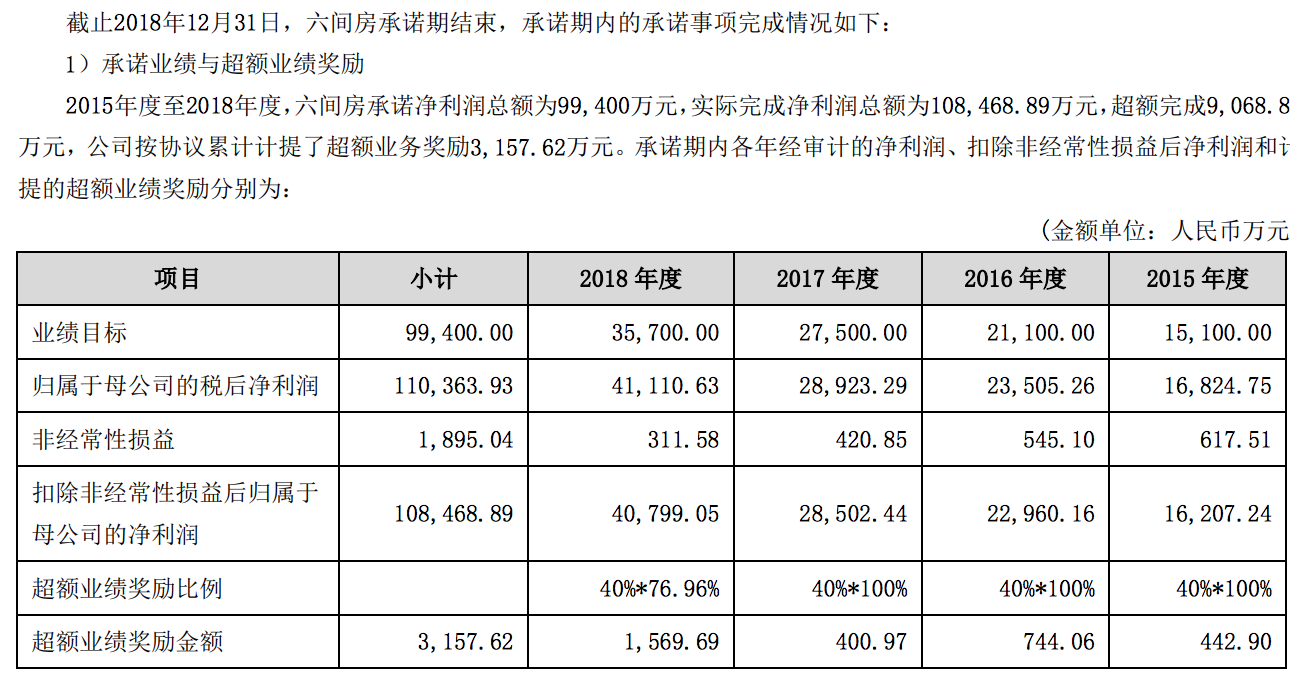
值得一提的是，2018年6月，宋城演艺公告对子公司六间房与密境和风进行重组，并在2019年4月完成，重组后为花房科技，以密境和风为会计主体（花房科技不再并表）。截至目前，宋城演艺持有花房科技37.06%股权。

 

2019年伊始，六间房仅实现净利润1.7亿元，同比2018年的4.1亿元下滑57.5%。而伴随着六间房不再并表，宋城演艺的营收及净利润增速双双下滑，其中营业收入下降18.67%，净利润同比增长率降至4%。

宋城演艺曾表示，若均不考虑数字娱乐平台以及六间房、花椒直播重组的财务数据，其2019年度实现营收22.32亿元，同比增长12.86%；净利润10.37亿元，同比增长17.24%。

根据宋城演艺近期的交流日志，宋城演艺称其预计花房科技2020年营收38亿元，同比增长 16%；净利润（剔除资产减值和股份支付摊销）约为3.8亿元，同比增长32%。

不过，宋城演艺也表示，由于行业盈利模式变化，从事移动端直播的花椒平台业绩增长，但从PC端直播起家的六间房平台业绩下滑，从而带来新花房科技主体对六间房的商誉减值压力。

东北证券在研报中称，花房科技对宋城演艺的业绩产生较大拖累，但仍维持“买入”评级。国信证券也认为，花房科技减值导致宋城演艺2020 年业绩显著承压，但有助于未来其聚焦主业轻装上阵谋发展。