LPL全球总决赛，EDG刷屏社交网络。

在B站、腾讯等直播平台，不仅各大游戏直播间人满为患，其它类直播间EDG相关话题也炙手可热；抖音、微博、朋友圈更纷纷刷出Z世代节日氛围。

与之鲜明对比的是，曾经的“直播界奥斯卡”花椒、六间房对此话题却冷冷清清，只有寥寥几人为EDG欢呼，让人不禁疑惑，这是“养生”的节奏？

近期，直播界“初代玩家”花房集团（下称花房）正在冲刺IPO，旗下拥有花椒、六间房等直播平台。

「不二研究」从其招股书发现， 花房收入结构较为单一，且高度依赖于单一平台。2018-2021前8个月，其9成营收依靠直播服务；若按照平台划分，近8成营收来源于花椒。

当直播赛道新玩家频出，多方夹击之下，Z世代的选择或将决定花房的生命周期。无论IPO成功与否，花房首先直面“初老”；毕竟，当EDG刷屏时，沉寂的花椒已经不复“直播界奥斯卡”。

初代直播平台IPO

花房的主营业务为国内花椒、六间房以及海外的HOLLA。

2006年，花房推出了六间房直播平台，也是直播界的“前辈”，经过一系列的思想碰撞，花椒于2015年诞生，由周鸿祎的“宝马车自燃”直播出圈，王思聪也空降直播间。

随着柳岩、李湘等明星的入驻，花椒逐渐声名大噪，2016年在京举行了一场知名主播云集的表演活动“花椒之夜”，被称为“直播界的奥斯卡”，并迎来了A轮投资。

2017年，花椒之夜就登陆北京卫视，打造了行业内首个直播节。

隔年6月，花椒与六间房联合，成为花房的两大主打平台；此后，花房为扩展海外业务，在2020年收购HOLLA集团，HOLLA也成为花房的第三个平台。

花房的股东架构中，“红衣教主”周鸿祎通过三六零(601360.SH)、花椒壹號等几家公司累计持股38.21%，为第一大股东。宋城演艺(300144.SZ)为第二大股东，持股37.06%。

截至2021年8月31日，花房注册用户达3.7亿，月活跃用户超5990万。

其中，花椒和六间房分别有2.07亿名和0.77亿名累计注册用户，花椒和六间房付费用户留存率分别为78.8%和66.1%。

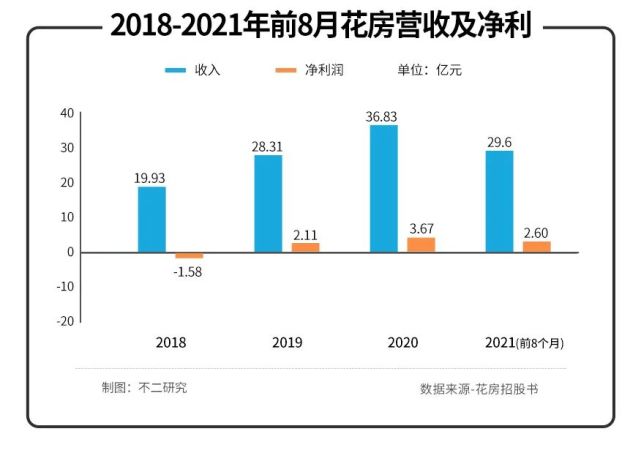
招股书显示，2018-2020年，及2021年前8个月，花房的收入分别为19.93亿元、28.31亿元、36.83亿元、29.6亿元，营收一直处于稳步上涨趋势。

反观其净利，2018-2020年，及2021年前8个月，花房经调整后的净利润分别为-1.58亿元、2.11亿元、3.67亿元、2.60亿元。

2019年，在与六间房合并的第二年，花房开始盈利。

作为直播平台，花房的推广及广告开支较高。据招股书数据显示，2018-2020年，推广及广告的开支分别为2.88亿元、3.15亿元、4.10亿元、3.37亿元；占总开支的84.6%、87%、90.9%、91.9%。

花房在招股书中解释，推广及广告开支是线上用户流量转介、线下营销活动产生的费用，及专门制作内容的相关成本。

当直播赛道竞争激烈，快手、抖音、腾讯、B站等互联网巨头，也开始入侵娱乐直播等垂直细分类直播。

在「不二研究」看来，作为娱乐直播界的“元老”，9成营收靠直播的花房正在经受竞争冲击；高额的推广及广告开支是个无底洞，其能否在资本加持下“突围”仍待考。

近8成营收依赖花椒

虚拟代币几乎是所有直播平台的主要收入来源。

花房在招股书中表示，其几乎所有收益产生自购买及向主播打赏虚拟物品以及直播产品上的其他服务。对于主播收到的虚拟物品产生的收益，花房与主播及其相关主播经纪公司进行分成。

花房收益主要产生自音视频直播服务、HOLLA集团提供的社交网络服务、其他服务。其中主要依赖音视频直播服务，又以花椒平台为主。

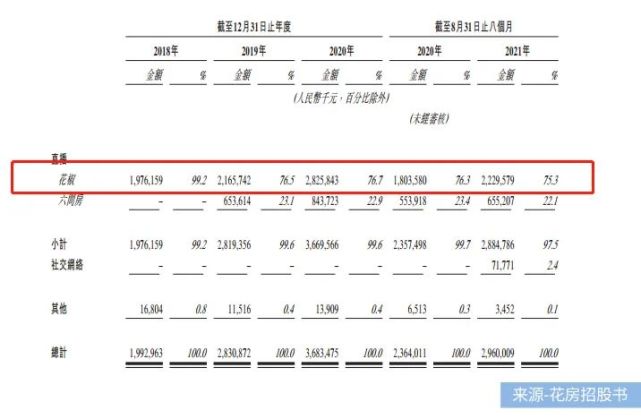
据招股书显示，花房的营收来源高度依赖于单一业务，其音视频直播收入在总营收占比超9成。2018年-2021年前8个月，直播收入分别占其总收入的99.2%，99.6%，99.6%，97.5%。

其中，花椒同期收益分别为19.76亿元、21.66亿元、28.26亿元、22.30亿元；分别占总收益的99.2%、76.5%、76.7%、75.3%。尽管与六间房合并，且有了海外业务，但花房的核心业务还是主要依赖花椒平台。

在花房的成本端，招股书披露主要源于主播成本、雇员开支、贷款费用、手续费等，尤以主播成本占比最大。

2018-2020年，及2021前8个月，主播成本分别为14.87亿元、19.20亿元、24.46亿元、19.56亿元；分别占总销售成本的87.9%、90.3%、91.5%、91.4%。

「不二研究」发现，此前，六间房的毛利率从2020年的的39.3%下降至2021年的35.2%。花房在招股书称，为提高用户参与度，六间房增加吸引及留任独立主播的成本。

营销费用、主播成本等逐年高企，花房也做出过转变。

从2019年开始，花房逐渐把采购额从2018年的以移动应用程序营销服务为主，逐步转到主播经纪公司服务。

2019-2020，及2021前8个月，最高采购额分别为1.31亿元、1.19亿元和1.18亿元。到2021年8月31日止，采购额全部转变为主播经纪公司服务。

与此同时，企查查数据显示，今年7月，花房经营范围新增演出经纪等，「不二研究」推测，花房或有意把多元化发展。

尽管演出经济逐渐成为大热门，但是巨头押注、竞争激烈，字节跳动、百度等的经营范围均新增演出经济，花房想要“多点开花”也很难。

在「不二研究」看来，作为“初代”直播平台，花房的盈利模式单一、营收来源单一等“致命伤”，为其埋下隐患；当娱乐直播下行，花房瞄准直播经纪服务；但与其他互联网巨头竞技时，却略显势单力薄。

淡出Z世代视线

据艾瑞咨询报告数据显示，中国视频直播市场预期将以2020年至2026年间23.0%的复合年增长率，于2026年达至5910亿元。

花房乘上了直播的风口，但双刃剑的另一面，是蜂拥而至的劲敌。

11月7日凌晨，有超10条与EDG有关的话题相继冲上微博热搜，即使是不关心电竞圈的朋友，EDG这个名字也无孔不入地进入了大脑。有大学生笑称：“睡的正香，被楼道的欢呼声吵醒了。”

打开各大社交软件，无论是朋友圈、B站、抖音、快手、Soul……都被EDG刷屏，虎牙更是豪甩20亿独揽LPL五年独播版权，可见其话题热度。

对比之下，花房就显得格外“清流”，打开花椒、六间房，只有寥寥几个用户改了EDG相关的名字，再无波澜。

在这个头部巨头疯抢、细分品类频出的直播风口，可以说是流量为王。这波热度不蹭，花房是跟不上时代了，还是独有清高？

映客、YY、一直播等平台持续发力，秀场、娱乐直播等屡见不鲜，短视频、社交平台也纷纷入场，甚至购物软件也培养出了李佳琦、薇娅等家喻户晓的主播……各行各业都盯上了直播这块“肉”。

对比之下，略显“年迈”的花房是否能跟上年轻的口味？

花房在招股书中表示，自身产品很受Z世代的喜爱。并有相关数据证明，截至2021年8月31日止8个月，很大一部分活跃用戶年龄在35岁及以下。

现今为止，最早一批Z世代，今年仅为26岁。花房招股书中，对于Z世代人群对自身产品喜好程度的判定，或与现实略有偏差。

「不二研究」随机采访了一位95年女性，提起花椒，她的第一反映是“擦边球”，并表示除此之外对花椒不甚了解。

企查查数据显示，今年6月，六间房某主播因表演中存在低俗行为被罚款，这并不是六间房第一次有主播被举报。

Z世代Katrina向「不二研究」表示，其更倾向选择抖音看直播，可以选择观看平时刷短视频时感兴趣的主播。如果是游戏的话会在斗鱼和虎牙，学习操作技巧，或是单纯的观赏。这次EDG的全球总决赛则是在B站上观看的，PC端更加的习惯。

直播仍是当下风口，但直播平台本身同质化严重；于互联网巨头而言，直播或是增加用户粘性的一种手段。在愈加激烈的竞争中，“初代”直播平台更是面临被多方夹击的风险。

当Z世代“后浪”纷纷奔向其它直播平台，花房的生命周期还能维持多久？

花房“花”已老

长江后浪推前浪。

抖音、B站、快手、虎牙等直播平台的崛起，纷纷收割Z世代的心。还有谁会记得直播场上，曾被称为“直播界奥斯卡”的花房呢？

六间房、花椒逐渐淡出年轻人的视线，虽然目前来看营收增速稳定，但“啃老”只会走向落幕，拥有“新鲜血液”才能葆青春。

当代“后浪”不断追逐新浪潮，花房渐显“初老”，即将面临被时代抛弃的危机。

在抗“初老”的路上，花房也在不断做出改变，转变自身的经营方向，开启多元化业务。是否能追上“后浪”的脚步，还需市场的检验。

本文部分参考资料：

1.《周鸿祎又一IPO，花椒直播和六间房能逆袭吗？》，深燃

2.《娱乐直播下行，周鸿祎的花房上市来迟》，商业数据派

不二研究郑重声明：文中观点系作者个人观点，不代表本平台就此提出任何投资建议。投资者应谨慎理性作出投资决策。

作者/秀一

排版/恩硕

监制/Yoda

出品/不二研究