写了一份适合刚入门脑电情绪识别的一个可用于练手的代码讲解。
首先再进行用脑电信号进行情绪识别时会对数据进行一个处理,比如计算出微分熵,功率谱图等。
在这里我们首先采用计算出微分熵DE。
微分熵
微分熵是香农信息熵在连续变量上的推广形式,设x为脑电信号,其原始表达式为:
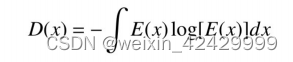
其中,E(x)指的是连续的脑电信号的概率密度函数.
微分熵的代码实现
def compute_DE(signal): #计算微分熵variance = np.var(signal, ddof=1)return math.log(2 * math.pi * math.e * variance) / 2带通滤波
def butter_bandpass(lowcut, highcut, fs, order=5): #带通滤波nyq = 0.5 * fslow = lowcut / nyqhigh = highcut / nyqb, a = butter(order, [low, high], btype='band')return b, adef butter_bandpass_filter(data, lowcut, highcut, fs, order=5):b, a = butter_bandpass(lowcut, highcut, fs, order=order)y = lfilter(b, a, data)return y什么要进行带通滤波呢?
因为对于原始数据,我们的目的是提取出四个频带(αβγθ)中的微分熵,所以我们要通过带通滤波从原始的信号中分离出这四个频带。(带通滤波器主要可以使用在需要保留的波的频率在一定的范围内,用于去除周围的噪声,可以起到良好的效果。)
加下来就是求出每次实验数据的微分熵了。
具体代码如下:
for trial in range(40): #对于其中40次试验, 这里是计算基线的DE特征temp_base_DE = np.empty([0]) #多一个基线DEtemp_base_theta_DE = np.empty([0]) #相对于seed数据集在频带上少一个deltatemp_base_alpha_DE = np.empty([0])temp_base_beta_DE = np.empty([0])temp_base_gamma_DE = np.empty([0])temp_de = np.empty([0, 120]) #将60S的数据进行一个切分,0.5s为一个点for channel in range(32): #对于40次试验中的每次试验中的32个通道trial_signal = data[trial, channel, 384:] #384之后的为试验数据base_signal = data[trial, channel, :384] #384 为3*128=384前三秒为试验前基线# ****************compute base DE****************base_theta = butter_bandpass_filter(base_signal, 4, 8, frequency, order=3) #这里是对基线信号的处理base_alpha = butter_bandpass_filter(base_signal, 8, 14, frequency, order=3)base_beta = butter_bandpass_filter(base_signal, 14, 31, frequency, order=3)base_gamma = butter_bandpass_filter(base_signal, 31, 45, frequency, order=3)base_theta_DE = (compute_DE(base_theta[:64]) + compute_DE(base_theta[64:128]) + compute_DE(base_theta[128:192]) + compute_DE(base_theta[192:256]) + compute_DE(base_theta[256:320]) + compute_DE(base_theta[320:])) / 6 #首先用0.5s将基线分成6段,然后对这六段的DE特征进行一个平均base_alpha_DE = (compute_DE(base_alpha[:64]) + compute_DE(base_alpha[64:128]) + compute_DE(base_alpha[128:192]) + compute_DE(base_theta[192:256]) + compute_DE(base_theta[256:320]) + compute_DE(base_theta[320:])) / 6base_beta_DE = (compute_DE(base_beta[:64]) + compute_DE(base_beta[64:128]) + compute_DE(base_beta[128:192]) + compute_DE(base_theta[192:256]) + compute_DE(base_theta[256:320]) + compute_DE(base_theta[320:])) / 6base_gamma_DE = (compute_DE(base_gamma[:64]) + compute_DE(base_gamma[64:128]) + compute_DE(base_gamma[128:192]) + compute_DE(base_theta[192:256]) + compute_DE(base_theta[256:320]) + compute_DE(base_theta[320:])) / 6temp_base_theta_DE = np.append(temp_base_theta_DE, base_theta_DE)temp_base_gamma_DE = np.append(temp_base_gamma_DE, base_gamma_DE)temp_base_beta_DE = np.append(temp_base_beta_DE, base_beta_DE)temp_base_alpha_DE = np.append(temp_base_alpha_DE, base_alpha_DE)theta = butter_bandpass_filter(trial_signal, 4, 8, frequency, order=3) #这是对实验数据的处理alpha = butter_bandpass_filter(trial_signal, 8, 14, frequency, order=3)beta = butter_bandpass_filter(trial_signal, 14, 31, frequency, order=3)gamma = butter_bandpass_filter(trial_signal, 31, 45, frequency, order=3)DE_theta = np.zeros(shape=[0], dtype=float)DE_alpha = np.zeros(shape=[0], dtype=float)DE_beta = np.zeros(shape=[0], dtype=float)DE_gamma = np.zeros(shape=[0], dtype=float)for index in range(120):DE_theta = np.append(DE_theta, compute_DE(theta[index * 64:(index + 1) * 64]))DE_alpha = np.append(DE_alpha, compute_DE(alpha[index * 64:(index + 1) * 64]))DE_beta = np.append(DE_beta, compute_DE(beta[index * 64:(index + 1) * 64]))DE_gamma = np.append(DE_gamma, compute_DE(gamma[index * 64:(index + 1) * 64]))temp_de = np.vstack([temp_de, DE_theta])temp_de = np.vstack([temp_de, DE_alpha])temp_de = np.vstack([temp_de, DE_beta])temp_de = np.vstack([temp_de, DE_gamma])temp_trial_de = temp_de.reshape(-1, 4, 120)decomposed_de = np.vstack([decomposed_de, temp_trial_de])#temp_base_DE = np.append(temp_base_DE, temp_base_theta_DE)temp_base_DE = np.append(temp_base_theta_DE, temp_base_alpha_DE)temp_base_DE = np.append(temp_base_DE, temp_base_beta_DE)temp_base_DE = np.append(temp_base_DE, temp_base_gamma_DE)base_DE = np.vstack([base_DE, temp_base_DE])最后我们得到的数据形式为【4800,128】
接下来我们要把数据规模改变为对应频带,电极二维映射的形式,也就是【4800,4,9,9】
也就是这种形式:
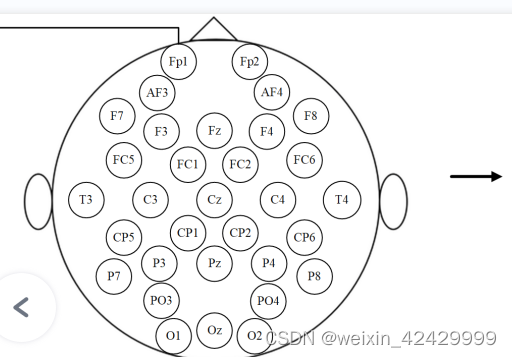

当我们把数据处理工作完成后,我们就可以把数据集划分为训练集以及测试集,(一般采用K折交叉验证。)然后把分好的数据放到网络里进行训练与测试 。
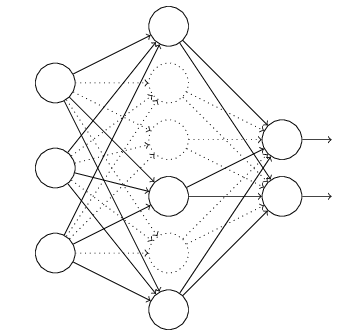
class ConvLSTM(nn.Module):def __init__(self, embedding_size, batch_size, num_classes, hidden_size=8, num_directions=1, num_layers=1):super(ConvLSTM, self).__init__()self.conv1 = nn.Conv2d(4, 24, 5)self.conv2 = nn.Conv2d(24, 128, 2)self.fc1 = nn.Linear(128 * 2 * 2, 96)self.fc2 = nn.Linear(96, embedding_size)self.lstm = nn.LSTM(embedding_size, hidden_size, num_layers, batch_first=True)self.hidden = Noneself.init_hidden(batch_size, hidden_size, num_directions, num_layers)self.fc3 = nn.Linear(hidden_size, num_classes)最后的结果为: