0.先上本节课目录:

1.函数二是函数一的导数
函数一: H e i g h t y ( x ) Height y(x) Heighty(x)
函数二: S l o p e s ( x ) Slope s(x) Slopes(x)
函数一 -> 函数二:
S l o p e s ( x ) = d y d x = l i m i t o f Δ y Δ x Slope s(x)=\frac{\operatorname dy}{\operatorname dx}=limit\ of\ \frac{\Delta y}{\Delta x} Slopes(x)=dxdy=limit of ΔxΔy
这里复习了导数,如果函数一是直线,直接用 Δ y Δ x \frac{\Delta y}{\Delta x} ΔxΔy就可以求出其导数,如果是曲线,就需要用极限求其导数。
2.函数一是函数二的积分
函数二 -> 函数一:
y ( x ) = ∫ s ( x ) d x y(x)=\int s(x)\operatorname dx y(x)=∫s(x)dx
这里介绍了积分符号。
3.求积分的方法A:反过来看什么函数的导数能得到积分的函数
大家都知道 y = x n y=x^n y=xn 的导数是 d y d x = n x n − 1 \frac{\operatorname dy}{\operatorname dx}=nx^{n-1} dxdy=nxn−1 ,反过来 d y d x = n x n − 1 \frac{\operatorname dy}{\operatorname dx}=nx^{n-1} dxdy=nxn−1 的积分是 y = x n y=x^n y=xn 。
那如果函数二是 d y d x = x n \frac{\operatorname dy}{\operatorname dx}=x^n dxdy=xn ,反推函数一应该含有 x n + 1 x^{n+1} xn+1 ,这里 x n + 1 x^{n+1} xn+1 求导后会有个系数 n + 1 n+1 n+1 ,所以函数一要再除以 n + 1 n+1 n+1 ,最终得到的积分是 y = 1 n − 1 x n + 1 y=\frac{1}{n-1}x^{n+1} y=n−11xn+1 。
这里其实就是用公式法,后续学习更多常见函数的求导公式后可以反推更多的积分公式。

4.例:通过代数方法求函数一
要考虑连续情形下的积分,先考虑单独间隔下的情况,然后缩小间隔,最后取极限使其连续。
先介绍单独间隔下的情况(算术方法),假设 y y y 之间的间隔( Δ x \Delta x Δx )都是单位1,求 s s s 就相当于求 Δ y \Delta y Δy ,有了 s s s 后也可以反推 y y y 。
y 0 1 4 9 16 → s 1 3 5 7 \begin{aligned} &y\quad0\quad1\quad4\quad9\quad16 \\ \rightarrow\quad&s\quad\quad1\quad3\quad5\quad7 \end{aligned} →y014916s1357
下面如果我们知道 s s s ,假设 y y y 是从0开始,变可以推出 y y y ,如下式所示。
→ y 0 4 7 9 10 10 s 4 3 2 1 0 \begin{aligned} \rightarrow\quad&y\quad0\quad4\quad7\quad9\quad10\quad10 \\ &s\quad\quad4\quad3\quad2\quad1\quad0 \end{aligned} →y04791010s43210

这里我们引入字母(代数方法),假设 y y y 之间的间隔( Δ x \Delta x Δx )还是是单位1,此时 y y y 不是从0开始了,我们只能求 y l a s t − y f i r s t y_{last}-y_{first} ylast−yfirst ,比如 y 2 − y 0 = ( y 1 − y 0 ) + ( y 2 − y 1 ) y_2-y_0=(y_1-y_0)+(y_2-y_1) y2−y0=(y1−y0)+(y2−y1) 。
y y 0 y 1 y 2 y 3 y 4 s ( Δ y ) y 1 − y 0 y 2 − y 1 y 3 − y 2 y 4 − y 3 \begin{aligned} &y\qquad y_0\qquad\quad y_1\qquad\quad y_2\qquad\quad y_3\qquad\quad y_4 \\ &s(\Delta y)\quad y_1-y_0\quad y_2-y_1\quad y_3-y_2\quad y_4-y_3 \end{aligned} yy0y1y2y3y4s(Δy)y1−y0y2−y1y3−y2y4−y3
∑ Δ y = y l a s t − y f i r s t \sum\Delta y=y_{last}-y_{first} \\ ∑Δy=ylast−yfirst

然后,我们要缩小间隔( Δ x \Delta x Δx ),此时 s s s 就要变为 Δ y Δ x \frac{\Delta y}{\Delta x} ΔxΔy ,乘以 Δ x \Delta x Δx 后得到 Δ y \Delta y Δy ,累加又可以获到 y l a s t − y f i r s t y_{last}-y_{first} ylast−yfirst 了。
∑ ( Δ y Δ x Δ x ) = y l a s t − y f i r s t \sum\left(\frac{\Delta y}{\Delta x}\Delta x\right)=y_{last}-y_{first} ∑(ΔxΔyΔx)=ylast−yfirst
当 Δ x \Delta x Δx 不断变小, Δ y Δ x \frac{\Delta y}{\Delta x} ΔxΔy 会不断接近 d y d x \frac{\operatorname dy}{\operatorname dx} dxdy ,下面就要讲到极限的情况。

5.例:通过微积分方法求函数一
上式在 Δ x → 0 \Delta x\rightarrow0 Δx→0 的情况下,求和转化为积分
∫ ( d y d x d x ) = y l a s t − y f i r s t \int\left(\frac{\operatorname dy}{\operatorname dx}\operatorname dx\right)=y_{last}-y_{first} ∫(dxdydx)=ylast−yfirst

6.求积分方法B:积分=函数一=函数二下的面积
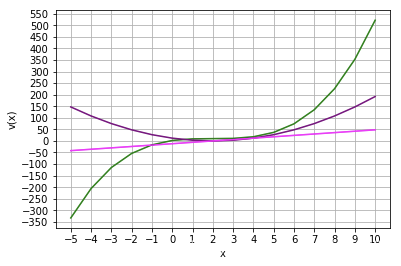
函数二: s ( x ) = 2 − 2 x s(x)=2-2x s(x)=2−2x
假设函数二是速度和时间的函数(这样更好理解),将时间四等分且假定速度在每个时间段( Δ x \Delta x Δx )中保持不变,如下图所示。下面将通过加法得到 y y y 值,此时得到的值并不精确,后面将不断缩小 Δ x \Delta x Δx 以获取精确的 y y y 值。

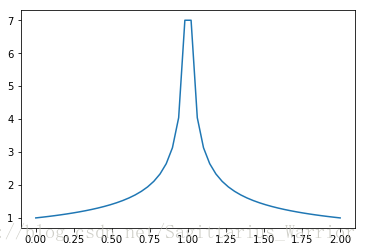
当 Δ x → 0 \Delta x \rightarrow0 Δx→0 时, y y y 就成了曲线 s ( x ) s(x) s(x) 下的面积, y ( 1 ) y(1) y(1) 就是三角形的面积 1 1 1 , y ( 1 / 2 ) y(1/2) y(1/2) 就是梯形面积 3 / 4 3/4 3/4 ,用公式法得到 y ( x ) = 2 x − x 2 y(x)=2x-x^2 y(x)=2x−x2 ,代入 1 1 1 和 1 / 2 1/2 1/2 结果与我们得到的面积相符。 y ( x ) y(x) y(x) 图像如下图所示。