Vue.js 2 所采用的双端 Diff 算法。既然快速 Diff 算法如此高效，我们有必要了解它的思路。接下来，我们就着重讨论快速 Diff 算法的实现原理。

相同的前置元素和后置元素

快速 Diff 算法借鉴了纯文本 Diff 算法中预处理的步骤。

案例：

旧的一组子节点:p-1、p-2、p-3。
新的一组子节点:p-1、p-4、p-2、p-3。

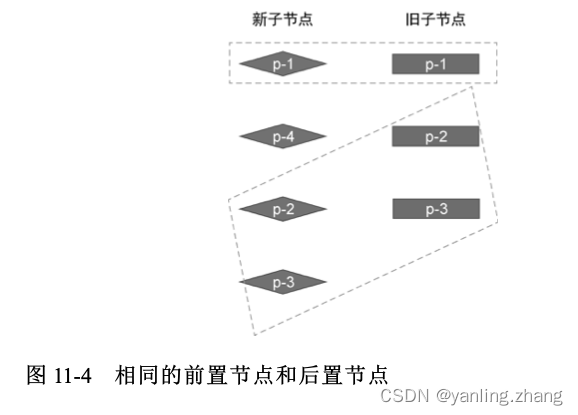
通过观察可以发现，两组子节点具有相同的前置节点 p-1，以及相同的后置节点 p-2 和 p-3，如图 下图 所示：
对于相同的前置节点和后置节点，由于它们在新旧两组子节点中的相对位置不变，所以我们无须移动它们，但仍然需要在它们之间打补丁。

处理前置节点

对于前置节点，我们可以建立索引 j，其初始值为 0，用来指向两组子节点的开头，如图 下图所示：

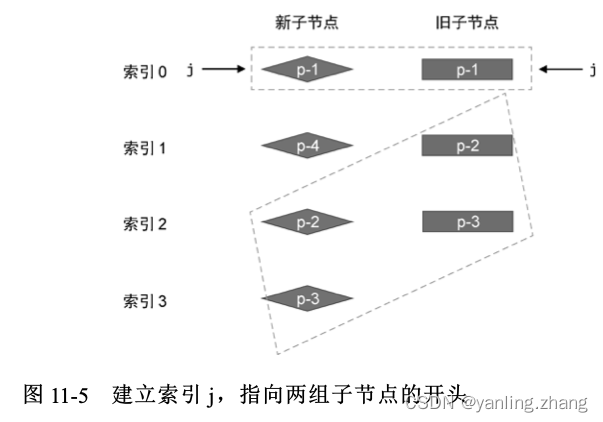
然后开启一个 while 循环，让索引 j 递增，直到遇到不相同的节点为止，如下面 patchKeyedChildren 函数的代码所示:

 function patchKeyedChildren(n1, n2, container) {const newChildren = n2.childrenconst oldChildren = n1.children// 处理相同的前置节点// 索引 j 指向新旧两组子节点的开头let j = 0let oldVNode = oldChildren[j]let newVNode = newChildren[j]// while 循环向后遍历，直到遇到拥有不同 key 值的节点为止while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新patch(oldVNode, newVNode, container)// 更新索引 j，让其递增j++oldVNode = oldChildren[j]newVNode = newChildren[j]}}

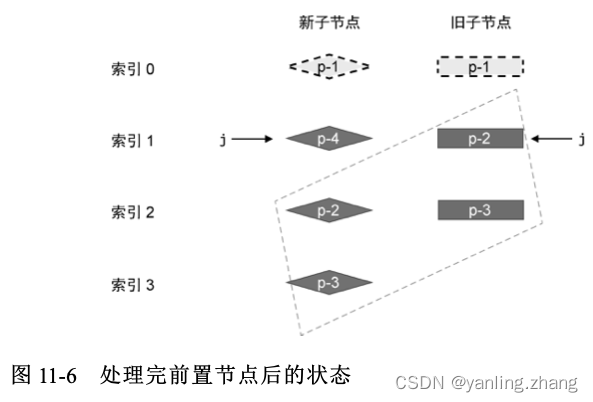
在上面这段代码中，我们使用 while 循环查找所有相同的前置节点，并调用 patch 函数进行打补丁，直到遇到 key 值不同的节点为
止。这样，我们就完成了对前置节点的更新。在这一步更新操作过后，新旧两组子节点的状态如图 下图 所示：

处理后置节点：

这里需要注意的是，当 while 循环终止时，索引 j 的值为 1。接下来，我们需要处理相同的后置节点。由于新旧两组子节点的数量可
能不同，所以我们需要两个索引 newEnd 和 oldEnd，分别指向新旧两组子节点中的最后一个节点，如图 下图 所示：

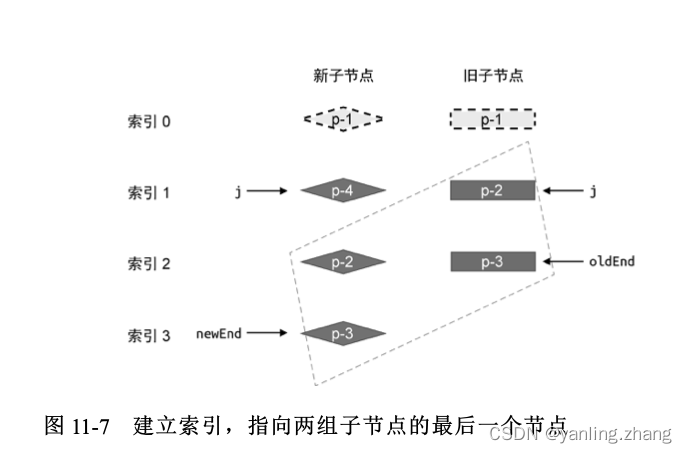
然后，再开启一个 while 循环，并从后向前遍历这两组子节点，直到遇到 key 值不同的节点为止，如下面的代码所示:

function patchKeyedChildren(n1, n2, container) {const newChildren = n2.childrenconst oldChildren = n1.children// 处理相同的前置节点// 索引 j 指向新旧两组子节点的开头let j = 0let oldVNode = oldChildren[j]let newVNode = newChildren[j]// while 循环向后遍历，直到遇到拥有不同 key 值的节点为止while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新patch(oldVNode, newVNode, container)// 更新索引 j，让其递增j++oldVNode = oldChildren[j]newVNode = newChildren[j]}+           // 处理后置节点：// 索引 oldEnd 指向旧的一组子节点的最后一个节点+           let oldEnd = oldChildren.length - 1// 索引 newEnd 指向新的一组子节点的最后一个节点+           let newEnd = newChildren.length - 1+           oldVNode = oldChildren[oldEnd]+           newVNode = newChildren[newEnd]// while 循环从后向前遍历，直到遇到拥有不同 key 值的节点为止+           while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新+               patch(oldVNode, newVNode, container)// 递减 oldEnd 和 nextEnd+              oldEnd --+              newEnd--+              oldVNode = oldChildren[oldEnd]+              newVNode = newChildren[newEnd]}}

与处理相同的前置节点一样，在 while 循环内，需要调用 patch函数进行打补丁，然后递减两个索引 oldEnd、newEnd 的值。在这一步更新操作过后，新旧两组子节点的状态如图 下图 所示：

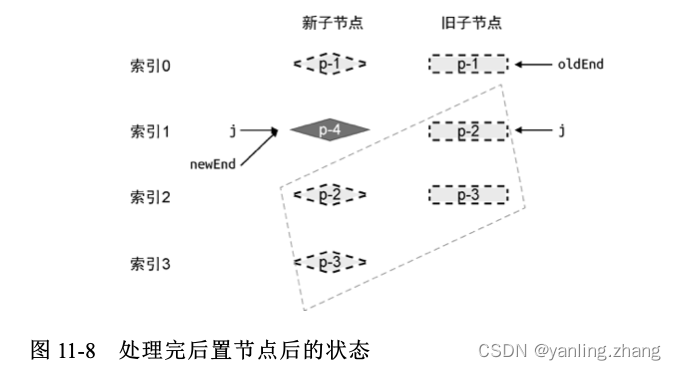
新增：

观察上图：当相同的前置节点和后置节点被处理完毕后，旧的一组子节点已经全部被处理了，而在新的一组子节点中，还遗留了一个未被处理的节点 p-4。其实不难发现，节点 p-4 是一个新增节点。那么，如何用程序得出“节点 p-4 是新增节点”这个结论呢?这需要我们观察三个索引 j、newEnd 和 oldEnd 之间的关系。

• 条件一： oldEnd < j成立:说明在预处理过程中，所有旧子节点都处理完毕了。
• 条件二：newEnd >= j成立:说明在预处理过后，在新的一组子 节点中，仍然有未被处理的节点，而这些遗留的节点将被视作新增节点。
  如果条件一和条件二同时成立，说明在新的一组子节点中，存在遗留节点，且这些节点都是新增节点。因此我们需要将它们挂载到正确的位置，如下图 所示：
  
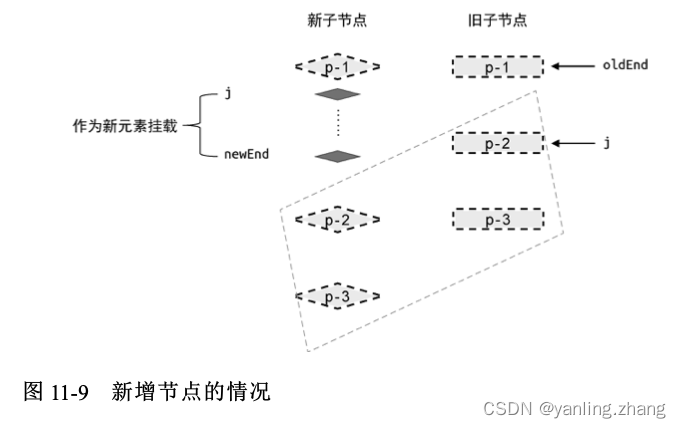
  在新的一组子节点中，索引值处于 j 和 newEnd 之间的任何节点都需要作为新的子节点进行挂载。那么，应该怎样将这些节点挂载到正确位置呢?这就要求我们必须找到正确的锚点元素。观察图 上图 中新的一组子节点可知，新增节点应该挂载到节点 p-2 所对应的真实DOM 前面。所以，节点 p-2 对应的真实 DOM 节点就是挂载操作的锚点元素。有了这些信息，我们就可以给出具体的代码实现了，如下所示:

function patchKeyedChildren(n1, n2, container) {const newChildren = n2.childrenconst oldChildren = n1.children// 处理相同的前置节点// 索引 j 指向新旧两组子节点的开头let j = 0let oldVNode = oldChildren[j]let newVNode = newChildren[j]// while 循环向后遍历，直到遇到拥有不同 key 值的节点为止while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新patch(oldVNode, newVNode, container)// 更新索引 j，让其递增j++oldVNode = oldChildren[j]newVNode = newChildren[j]}// 处理后置节点：// 索引 oldEnd 指向旧的一组子节点的最后一个节点let oldEnd = oldChildren.length - 1// 索引 newEnd 指向新的一组子节点的最后一个节点let newEnd = newChildren.length - 1oldVNode = oldChildren[oldEnd]newVNode = newChildren[newEnd]// while 循环从后向前遍历，直到遇到拥有不同 key 值的节点为止while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新patch(oldVNode, newVNode, container)// 递减 oldEnd 和 nextEndoldEnd --newEnd--oldVNode = oldChildren[oldEnd]newVNode = newChildren[newEnd]}// 新增// 预处理完毕后，如果满足如下条件，则说明从 j --> newEnd 之间的节点应作 为新节点插入+          if(j > oldEnd && j <= newEnd) {// 锚点索引+              const anchorIndex = newEnd + 1// 锚点元素+              const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null+              while(j <= newEnd) {+                  patch(null, newChildren[j++], container, anchor)+              }}}

在上面这段代码中，首先计算锚点的索引值(即 anchorIndex) 为newEnd + 1。如果小于新的一组子节点的数量，则说明锚点元素 在新的一组子节点中，所以直接使用 newChildren[anchorIndex].el 作为锚点元素;否则说明索引 newEnd 对应的节点已经是尾部节点了，这时无须提供锚点元素。有了 锚点元素之后，我们开启了一个 while 循环，用来遍历索引 j 和索引 newEnd 之间的节点，并调用 patch 函数挂载它们。

删除

案例：

• 旧的一组子节点:p-1、p-2、p-3。
• 新的一组子节点:p-1、p-3。

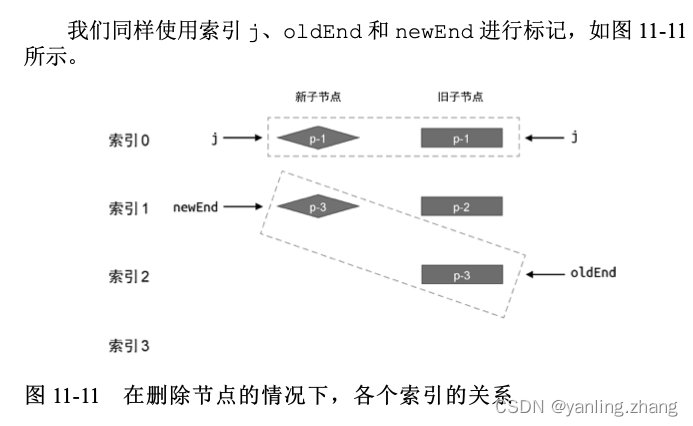
当前置节点，后置节点都处理完成，后剩余未被处理的节点如下图所示：

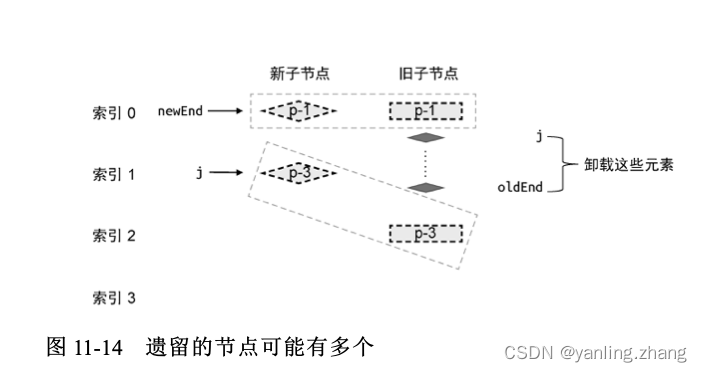
索引 j 和索引 oldEnd 之间的任何节点都应该被卸载，具体实现如下:

function patchKeyedChildren(n1, n2, container) {const newChildren = n2.childrenconst oldChildren = n1.children// 处理相同的前置节点// 索引 j 指向新旧两组子节点的开头let j = 0let oldVNode = oldChildren[j]let newVNode = newChildren[j]// while 循环向后遍历，直到遇到拥有不同 key 值的节点为止while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新patch(oldVNode, newVNode, container)// 更新索引 j，让其递增j++oldVNode = oldChildren[j]newVNode = newChildren[j]}// 处理后置节点：// 索引 oldEnd 指向旧的一组子节点的最后一个节点let oldEnd = oldChildren.length - 1// 索引 newEnd 指向新的一组子节点的最后一个节点let newEnd = newChildren.length - 1oldVNode = oldChildren[oldEnd]newVNode = newChildren[newEnd]// while 循环从后向前遍历，直到遇到拥有不同 key 值的节点为止while(oldVNode.key === newVNode.key) {// 调用 patch 函数进行更新patch(oldVNode, newVNode, container)// 递减 oldEnd 和 nextEndoldEnd --newEnd--oldVNode = oldChildren[oldEnd]newVNode = newChildren[newEnd]}// 新增// 预处理完毕后，如果满足如下条件，则说明从 j --> newEnd 之间的节点应作 为新节点插入if(j > oldEnd && j <= newEnd) {// 锚点索引const anchorIndex = newEnd + 1// 锚点元素const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : nullwhile(j <= newEnd) {patch(null, newChildren[j++], container, anchor)}+         } else if (j > newEnd && j <= oldEnd) {// 删除// j -> oldEnd 之间的节点应该被卸载+            while(j <= oldEnd) {+                unmount(oldChildren[j++])}}}

在上面这段代码中，我们新增了一个 else…if 分支。当满足条件j > newEnd && j <= oldEnd时，则开启一个while循环，并调用unmount 函数逐个卸载这些遗留节点。

移动

有点复杂