前言

今天我们要说的就是数值微积分，赶紧看看他和高等数学中的微积分有什么区别吧。本文是科学计算与MATLAB语言专题六第一小节的学习笔记，如果大家有时间的话，可以去听听课，没有的话，可以看看我的笔记，还是很不错的。

1 数值微分

（1）数值差分与差商
微积分中，任意函数$f（x）$在$x_0$点的导数是通过极限定义的：
$f^{\prime }（x_0）=\underset{t\to 0}{\lim }\frac{f（x_0+h）-f（x_0）}{h}$
$f^{\prime }（x_0）=\underset{t\to 0}{\lim }\frac{f（x_0）-f（x_0-h）}{h}$
$f^{\prime }（x_0）=\underset{t\to 0}{\lim }\frac{f（x_0+h/2）-f（x_0-h/2）}{h}$
如果去掉极限定义中h趋向于0的极限过程，得到函数在$x_0$点处以h（h>0）为步长的向前差分、向后差分和中心差分公式：
向前差分：$\Delta r（x_0）=f（x_0+h）-f（x_0）$
$\Delta$原来她叫Delta
向后差分：$\nabla P（x_0）=f（x）-f（x_0-h）$
$\nabla$她叫nabla
中心差分：$\delta F（x_0）=f（x_0+h/2）-f（x_0-h/2）$
$\delta$她叫delta
当步长h充分小时，得到函数在$x_0$点处以h（h>0）为步长的向前差商、向后差商和中心差商公式：
向前差分：$f^{\prime }（x_0）\approx f（x_0+h）-f（x_0）$
向后差分：$f^{\prime }（x_0）\approx f（x）-f（x_0-h）$
中心差分：$f^{\prime }（x_0）\approx f（x_0+h/2）-f（x_0-h/2）$
函数f（x）在点x0的微分接近于函数在该点的差分，而f在点x的导数接近于函数在该点的差商。
（2）数值微分的实现
MATLAB提供了求向前差分的函数diff，其调用格式有三种：
dx=diff（x）：计算向量x的向前差分，dx（i）=x（i+1）-x（i），i=1，2，…，n-1。
dx=diff（x，n）：计算向量x的n阶向前差分。例如，diff（x，2）=diff（diff（x））。
dx=diff（A，n，dim）：计算矩阵A的n阶差分，dim=1时（默认状态），按列计算差分；dim=2，按行计算差分。
注意：diff函数计算的是向量元素间的差分，故差分向量元素的个数比原向量少了一个。同样，对于矩阵来说，差分后的矩阵比原矩阵少了一行或一列。
另外，计算差分之后，可以用f（x）在某点处的差商作为其导数的近似值。
例1 设f(x)=sinx，在[0，2π]范围内随机采样，计算f’(x)的近似值，并与理论值f’(x)=cosx 进行比较。

x=[0,sort(2*pi*rand(1,5000)),2*pi];
y=sin(x);
f1=diff(y)./diff(x);
f2=cos(x(1:end-1));
plot(x(1:end-1),f1,x(1:end-1),f2);
d=norm(f1-f2)

d =0.0456

2 数值积分

2.数值积分
（1）数值积分基本原理
在高等数学中，计算定积分依靠微积分基本定理，只要找到被积函数f（x）
的原函数大（x），则可用牛顿一莱布尼兹（Newton-Leibniz）公式：
$${\int }_a^{b}f（x）dx=F（b）-F（a）$$在有些情况下，应用牛顿一莱布尼兹公式有困难，例如，当被积函数的原函数无法用初等函数表示，或被积函数是用离散的表格形式给出的。这时就需要用数值解法来求定积分的近似值。
求定积分的数值方法多种多样，如梯形法、辛普森（Simpson）法、高斯求积公式等。它们的基本思想都是将积分区间[a，b]分成n个子区间$[x_i，x_{i+1}]$，i=1，2，…，n，其中$x_i=a$，$x_{i+1}=b$，这样求定积分问题就分解为下面的求和问题：
$$S={\int }_a^{b}f（x）dx=\sum _{i=1}^n{\int }_{x_i}^{x_{i+1}}f（x）dx$$在每一个小的子区间上定积分的值可以近似求得，从而避免了牛顿一莱布尼兹公式需要寻求原函数的困难。
（2）数值积分的实现
基于自适应辛普森方法
[I，n]=quad（filename，a，b，tol，trace）
基于自适应Gauss-Lobatto方法
[I，n]=quad1（filename，a，b，tol，trace）
其中，filename是被积函数名；
a和b分别是定积分的下限和上限，积分限[a，b]必须是有限的，不能为无穷大（Inf）；
tol用来控制积分精度，默认时取tol=$10^{-6}$；
trace控制是否展现积分过程，若取非0则展现积分过程，取0则不展现，默认时取trace=0；返回参数I即定积分的值，n为被积函数的调用次数。
例2 分别用quad函数和quadl函数求定积分${\int }_0^1\frac{1}{1+x^2}dx$的近似值，并在相同的积分精度下，比较被积函数的调用次数。

format long%有效数字保留16位。
f=@(x) 4./(1+x.^2);
[I,n]=quad(f,0,1,1e-8)%基于自适应辛普森方法求近似值。
[I,n]=quadl(f,0,1,1e-8)%基于自适应Gauss-Lobatto方法求近似值。
(atan(1)-atan(0))*4%求理论值。
format short%format short：恢复默认格式，小数点后保留4位。

I =3.141592653733437
n =61
I =3.141592653589806
n =48
ans =3.141592653589793

基于全局自适应积分方法
I=integral（filename，a，b）
其中，I是计算得到的积分；
filename是被积函数；
a和b分别是定积分的下限和上限，积分限可以为无穷大。
例3 求定积分$I={\int }_1^{e}f=\frac{1}{(x\sqrt{(1-{\ln }^{2}x))}}$。
被积函数文件fe.m：

function f=fe(x)
f=1./(x.*sqrt(1-log(x).^2));
I=integral(@fe,1,exp(1))

基于自适应高斯-克朗罗德方法
[I，err]=quadgk（filename，a，b）
其中，err返回近似误差范围，其他参数的含义和用法与quad函数相同。积分上下限可以是无穷大（-Inf或Inf），也可以是复数。如果积分上下限是复数，则quadgk函数在复平面上求积分。
例4 求定积分${\int }_{\frac{2}{\pi }}^{+\infty }f=\frac{1}{x^2}sin\frac{1}{x}dx$。
被积函数文件fsx.m：

function f=fsx(x)
f=sin(1./x)./x.^2;

>>I=quadgk(@fsx,2/pi,+Inf)
I =1.0000

基于梯形积分法
已知$（x_i，y_i）（i=1，2，\dots ，n）$，且$a=x_1<x_2<\dots <x_n=b$，求$I={\int }_a^{b}f（x）dx$近似值。
I=trapz（x，y）
其中，向量x、y定义函数关系y=f（x）。
trapz函数采用梯形积分法则，积分的近似值为：
$$I=\sum _{i=1}^{n-1}{h}_i\frac{y_{i+1}+y_i}{2}$$其中，$h_i=x_{i+1}-x_i$。
可用以下语句实现：
sum（diff（x）.*（y（1：end-1）+y（2：end））/2）)
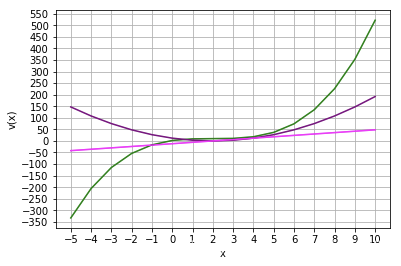
例5 设x=1:6，y=[6,8,11,7,5,2],用trapz函数计算定积分。

x=1:6;
y=[6,8,11,7,5,2];
plot(x,y,'-ko');
grid on
axis([1,6,0,11]);
I1=trapz(x,y)
I2=sum(diff(x).*(y(1:end-1)+y(2:end))/2)

（3）多重定积分的数值求解
求二重积分的数值解：${\int }_c^d{\int }_a^{b}f（x，y）dxdy$
I=integral2（filename，a，b，c，d）
I=quad2d（filename，a，b，c，d）
I=dblquad（filename，a，b，c，d，tol）
求三重积分的数值解：${\int }_e^f{\int }_c^d{\int }_a^{b}f（x，y，z）dxdydz$
I=integra13（filename，a，b，c，d，e，f）
I=triplequad（filename，a，b，c，d，e，f，tol）
例6 分别求二重积分和三重积分。
$${\int }_{-1}^1{\int }_{-2}^2{e}^{-x^2/2}sin(x^2+y)dxdy$$
$${\int }_0^1{\int }_0^{\pi }{\int }_0^{\pi }4xz{e}^{-z^{2}y-x^2}dxdydz$$

f1=@(x,y) exp(-x.^2/2).*sin(x.^2+y);
I1=quad2d(f1,-2,2,-1,1)
f2=@(x,y,z) 4*x.*z.*exp(-z.*z.*y-x.*x);
I2=integral3(f2,0,pi,0,pi,0,1)

小结

大家学会了吗？最后欢迎大家
点赞👍，收藏⭐，转发🚀，
如有问题、建议，请您在评论区留言💬哦。