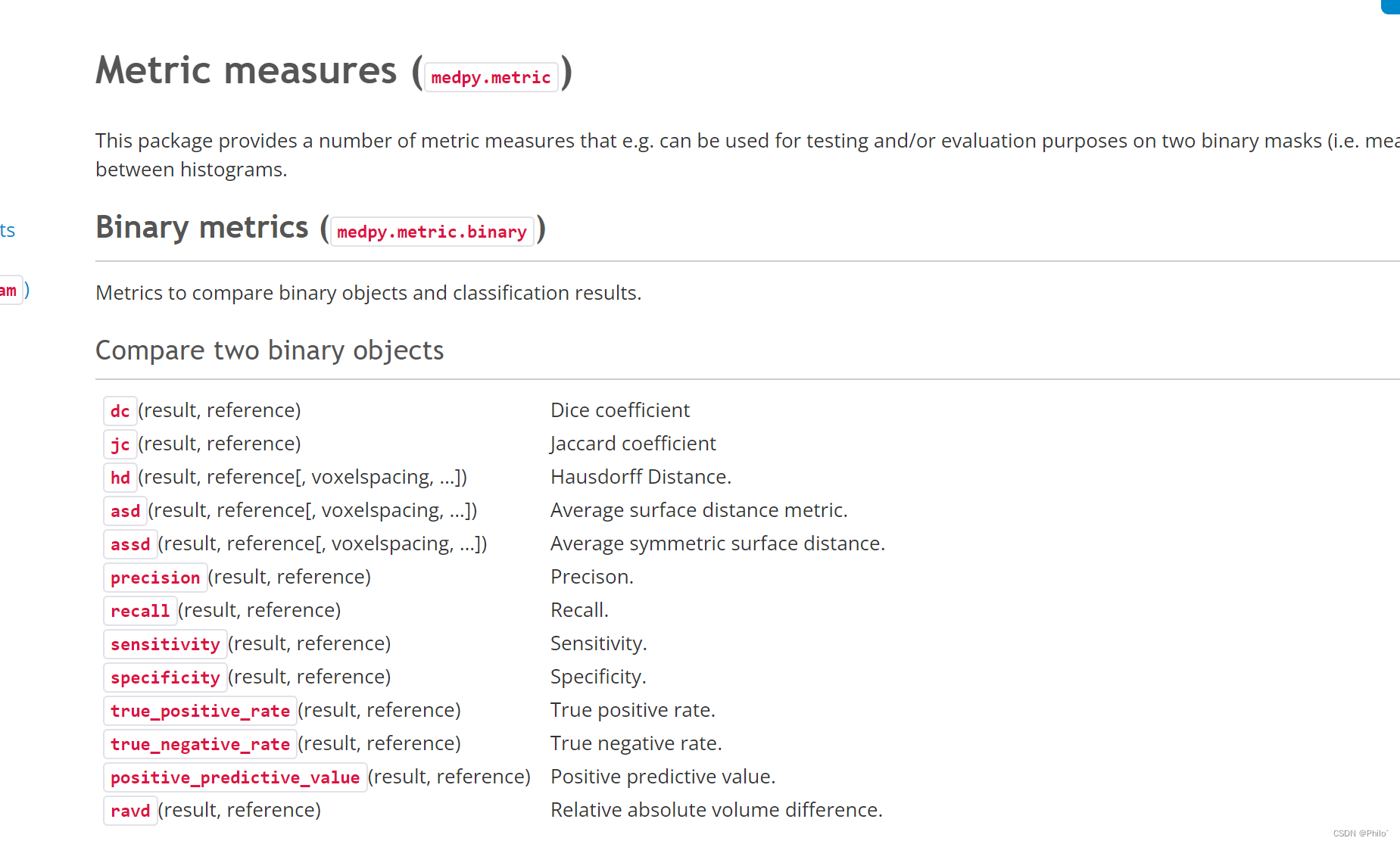
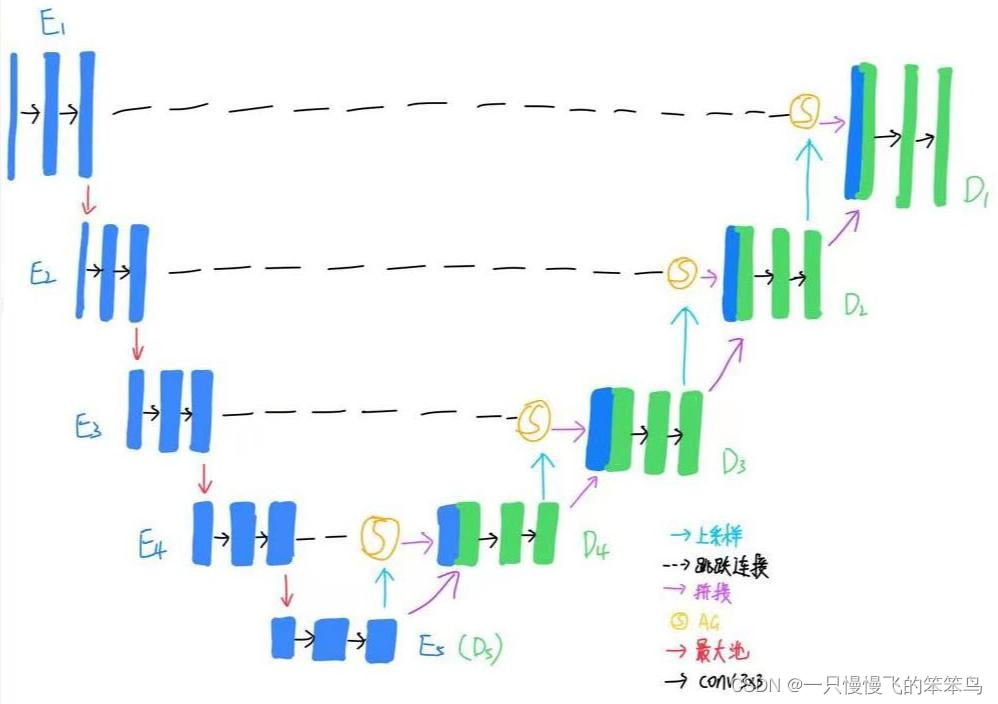
TverskyLoss提出的初衷是为了解决数据的类不平衡现象的,其在精度和召回率之间取得了较好的平衡
精度:预测正确的数量/所有的数量
召回率:预测正确的数量/所有正确的数量
如果不平衡标签,学习过程可能会收敛到次优损失函数的局部极小值,因此预测可能会强烈偏向非损伤组织。结果将是高精度、低召回率的分割
解决数据不平衡的一种常用方法,特别是体素方法,是从每个类中提取相等的训练样本。这种方法的缺点是它没有使用图像的所有信息内容,并且可能偏向于很少的类
Dice Loss是precision和recall的调和平均值,对FPs和FNs的权重相等。为了更好地权衡精确性和召回率(FPs与FNs),我们提出了基于Tversky相似性指数的损失层。Tversky指数是骰子相似系数和Fβ得分的推广。下面介绍如何调整这个损失函数的超参数,以便在训练一个高度不平衡的数据中表现良好的网络时将重点放在假阴性。
方法
设P和G分别是预测值和真实值Ground truth值的集合,则Dice相似度系数表示为:
上面这个式子中的FPS(精确率)和FNs(召回率)的权重是相同的,为了使得在训练过程中召回率的权重高于精确率,基于Tversky系数提出了一个损失层,Tiversky index定义如下:
其中α和β分别控制着精确率和召回率的惩罚大小。
Tversky Loss损失函数的定义为:
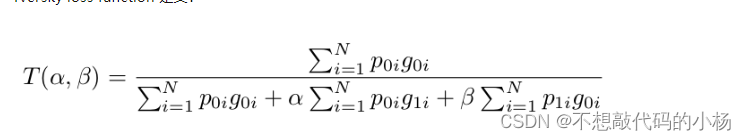
其中

通过调整超参数α和β,我们可以控制假阳性和假阴性之间的权衡。
值得注意的是,在α=β=0.5时 Tversky指数为与Dice系数相同,也等价于 F1 score。当α=β=1时,等式2产生Tanimoto系数,设置α+β=1产生Fβ scores。βs越大,召回率越高(通过更加强调假阴性)。我们假设在我们的广义损失函数中使用更高的βs将导致对不平衡数据的更高的泛化和更好的性能,并有效地帮助我们将重点转移到降低FNs和提高召回率。
F1-socre是精确率和召回率的调和平均数

Tanimoto系数可以判断两个数据的相关程度,Tanimoto系数可以表示为两个集合的交集比上两个集合的并集。举例:
两个人拥有相同的东西/两个人所有的东西
可以看出两个人的相关程度,如果拥有相同东西越多表明两个人的兴趣爱好越相同(一般情况下)

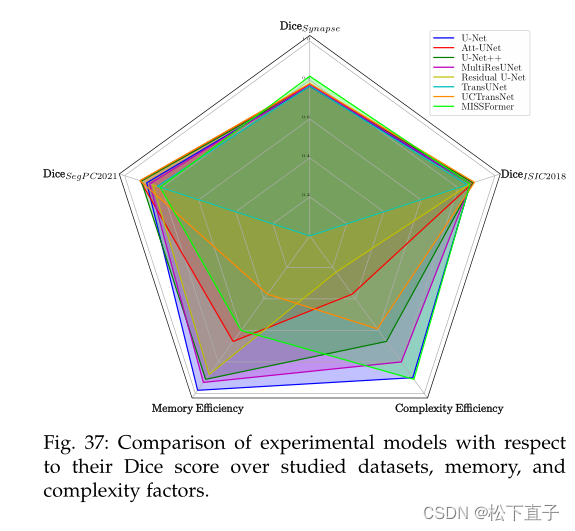
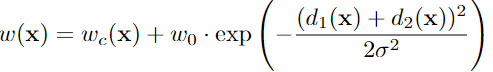


![[转]医学图像分割综述](https://img-blog.csdnimg.cn/20190730135615475.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MDc3OTcyNw==,size_16,color_FFFFFF,t_70)